Inhaltsverzeichnis
Himmelsmechanik
Einleitung
Die Himmelsmechanik befasst sich mit den Bahnbewegungen der Himmelskörper und hat einen physikalischen Hintergrund. Die Bahnbestimmung gehört ebenfalls zur Himmelsmechanik. Diese Disziplin der Astronomie bildet die Basis für die darauf aufbauende Ephemeridenrechnung. Die Ephemeridenrechnung selbst bewegt sich auf dem Gebiet der Positionsbestimmungen von der Sonne, dem Mond, den Planeten, den vielen Kleinkörpern und ist eher mathematischer Natur. Der Übergang zwischen den beiden Gebieten ist jedoch fließend, eine genaue Abgrenzung existiert nicht.
Energiegleichung
Hat man die Koordinaten $\vec{r}$ und $\dot{\vec{r}} = \vec{v}$, so kann man die kinetische Energie $T$ und die potentielle Energie $V \lt 0$ mit der folgenden Beziehung berechnen:
$$E = T + V = \frac{1}{2}\cdot m\cdot v^2 + V(r)\tag{1}$$
mit $\vec{v}\cdot\vec{v} = v^2$ und $E$ als der Gesamtenergie. Sie wird noch als Erhaltungsgrösse der Zeit $t$ behandelt. Die Ableitung nach der Zeit $t$ und Teilung durch den Impuls $\vec{p} = m\cdot\vec{v}$ ergibt eine Differentialgleichung 2. Ordnung:
$$0 = \ddot{r} + \frac{1}{m}\cdot\frac{d}{dr}V(r)\tag{2}$$
Daraus ergeben sich die Newtonschen Kraftgleichungen:
$$F = m\cdot \ddot{r} \qquad \text{und}\qquad K = - \frac{d}{dr}V(r)\tag{3}$$
mit $F + K = 0$.
Es ist auch umgekehrt die Integration der Energiegleichung (1) möglich:
$$p = \sqrt{2\cdot m}\cdot \int \sqrt{E - V(r)}\; \text{d}r\tag{4}$$
und
$$t = \sqrt{\frac{m}{2}}\cdot \int \frac{1}{\sqrt{E - V(r)}}\; \text{d}r\tag{5}$$
Generalisierte Koordinaten
Die Koordinaten $\vec{r}$ und $\vec{v}$ sind:
$$\vec{r} = r\cdot \left(\begin{split} & \cos(\nu) \\ & \sin(\nu) \end{split}\right)\tag{6}$$
$$\vec{v} = \dot{\vec{r}} = \dot{r}\cdot \left(\begin{split} & \cos(\nu) \\ & \sin(\nu) \end{split}\right) + r\cdot\dot{\nu}\cdot \left(\begin{split} - & \sin(\nu) \\ + & \cos(\nu) \end{split}\right)\tag{7}$$
Daraus folgt für $v^2$:
$$v^2 = \dot{r}^2 + r^2\cdot\dot{\nu}^2\tag{8}$$
Die modifizierte Energiegleichung lautet dann:
$$E = \frac{1}{2}\cdot m\cdot\dot{r}^2 + \frac{1}{2}\cdot m\cdot r^2\cdot \dot{\nu}^2 + V(r)\tag{9}$$
Keplergesetze
1. Keplergesetz: Alle Planeten bewegen sich auf elliptischen Bahnen, in deren einem der beiden Brennpunkte sich die Sonne befindet.
$$r = \frac{p}{1 + \epsilon\cdot\cos(\nu)}\tag{10}$$
Zur Geometrie der Ellipse und den Parametern siehe Kegelschnitte.
2. Keplergesetz: Ein von der Sonne zum Planeten gezogener Fahrstrahl (Radius) überstreicht in gleichen Zeiten gleichgrosse Flächenabschnitte $\vec{F}$.
$$\vec{F} = \frac{\vec{L}_{\nu}}{2\cdot m}\cdot T\tag{11} \qquad\text{mit}\qquad T = t_1 - t_2$$
 Abb. 1: Das 2. Keplergesetz. Die hellblauen Flächen sind die Flächenabschnitte $\vec{F}$.
Abb. 1: Das 2. Keplergesetz. Die hellblauen Flächen sind die Flächenabschnitte $\vec{F}$.
$\nu$ = wahre Anomalie
 Abb. 2: Der Flächensatz vom 2. Keplergesetz
Abb. 2: Der Flächensatz vom 2. Keplergesetz
Abb.2: Eine anschauliche Darstellung des Drehimpulses $\vec{L_{\nu}}$ und des zweiten Keplergesetzes. Die vom Radiusvektor $r$ in der Zeit $\mathrm{d}t$ überstrichene Fläche $\vec{H}$ ist gleich der halben Fläche (zwischen den Punkten $A$, $B$ und $C$) des Parallelogramms. Der Drehimpuls ist zeitlich konstant.
3. Keplergesetz: Das Quadrat der Umlaufzeit $U$ eines Planeten verhält sich wie der Kubus (dritte Potenz) seines mittleren Bahnabstands.
$$\frac{U^2}{r^3} = \frac{4\cdot\pi^2}{G\cdot M_S}\tag{12}$$
Formt man das 3. Keplergesetz für $r = a = 1 \text{AE}$ um zu
$$U_s = \frac{2\pi}{k}\tag{13}$$
so erhält man die siderische Umlaufszeit $U_s$ der Erde. Die gaußsche Gravitationskonstante $k = \sqrt{G\cdot M_S}$ ist als eine fundamentale Naturkonstante für die Stärke der Gravitation verantwortlich.
Sie ist definiert mit
$$k = \frac{2\pi}{U_s}\tag{14}$$
und $U_s$ als das siderische Jahr.
$$\deg(k) = n = \frac{360^{\circ}}{U_s}\tag{15}$$
liefert die mittlere tägliche Bewegung $n$ der Erde um die Sonne.
Die Herleitung: Beruhend auf der Energiebilanzgleichung $E$ mit dem Gravitationpotential $$V(r) = - G\cdot \frac{m\cdot M_S}{r}\tag{16}$$
$$E = \frac{1}{2} \cdot m\cdot \dot{r}^2 + \frac{1}{2}\cdot m\cdot r^2 \dot{\nu}^2 - G\cdot \frac{m\cdot M_S}{r}\tag{17}$$
resultiert aus der Ableitung nach $r$ die Zentripetalkraft $\vec{F}_z$ (links) bzw. die Gravitationskraft $\vec{F}_g$ (rechts):
$$F_z = m\cdot\dot{\nu}^2\cdot r = - F_g = G\cdot\frac{M\cdot m}{r^2} \Leftrightarrow \frac{U^2}{r^3} = \frac{4\pi^2}{G\cdot M} = \text{konst.}$$
mit $\dot{\nu} = \omega = \frac{2\pi}{U}\tag{18}$
Das Verhältnis der Umlaufszeit $U$ zur Bahngrösse $r$ ist zeitlich konstant und damit eine Erhaltungsgrösse. In einem Relativsystem mit $r = r_1 - r_2$ gilt, wobei man in vielen Anwendungen die kleinere Masse nicht vernachlässigen kann: $$\frac{U^2}{r^3} = \frac{4\pi^2}{G\cdot \left(m_1 + m_2\right)}\tag{19}$$
Graphische Darstellung:
Bahnen gleicher Energie haben die gleiche große Halbachse.
 Abb. 3: Bahnen gleicher Energie haben die gleiche große Halbachse
Abb. 3: Bahnen gleicher Energie haben die gleiche große Halbachse
Bahnen gleicher Flächenkonstante (Drehimpulskonstante). Der Schnittpunkt aller Bahnkurven gleicher Flächenkonstanten $h$ liegt bei
$$\displaystyle r\left(\varphi = \frac{\pi}{2}\right) = k = \frac{h^2}{G\cdot M_S}$$
mit $h = \frac{L}{m}\dots$ als der Drehimpulskonstanten.
 Abb. 4: Bahnen gleicher Flächenkonstante (Drehimpulskonstante)
Abb. 4: Bahnen gleicher Flächenkonstante (Drehimpulskonstante)
Alle in den Abbildungen 3 und 4 gezeigten Bahnen fallen im Brennpunkt zusammen.
Runge-Lenz Vektor
Der Runge-Lenz Vektor $\vec{A}$ (Abb.2) ist wie $E$ und $L_{\nu}$ eine Erhaltungsgrösse.
$$\vec{A} = (m\cdot\dot{\vec{r}} \times \vec{L}_{\nu}) - G\cdot M_S\cdot m^2\cdot \frac{\vec{r}}{r} = \text{konst.}\tag{20}$$
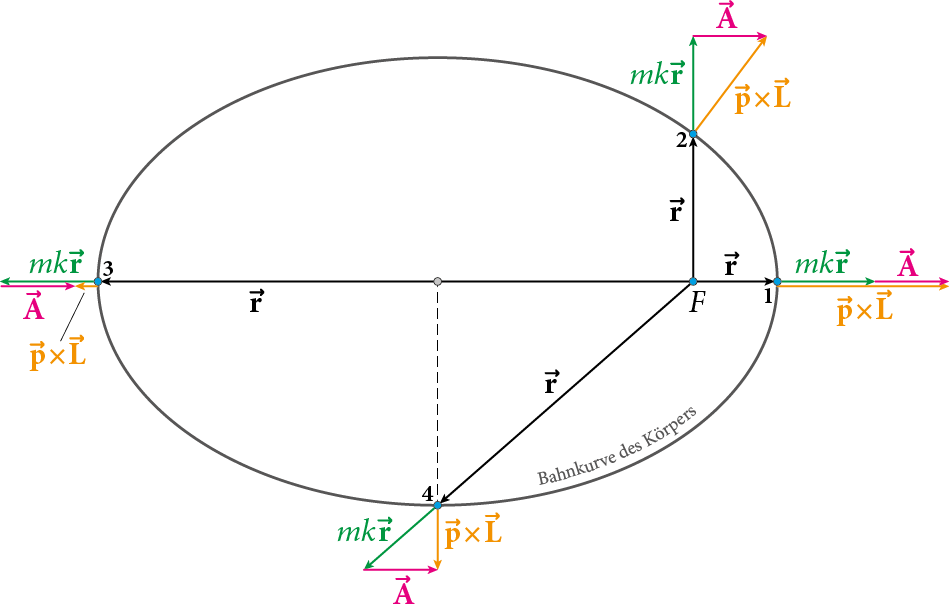 Abb. 5: Der Laplace-Runge-Lenz-Vektor A
Abb. 5: Der Laplace-Runge-Lenz-Vektor A
Der Runge-Lenz Vektor wird auch als Perizentrumsvektor bezeichnet, weil er die in Richtung des Perihels der Planetenbahn zeigt. Nach skalarer Multiplikation mit $\vec{r}$ unter Berücksichtigung der nachfolgenden Relationen
$$\vec{r}\cdot\vec{A} = r\cdot A\cdot\cos(\nu), \quad \vec{r}\cdot\vec{r} = |\vec{r}|^2 = r^2\tag{21}$$
und
$$\vec{r}\cdot (m\cdot\dot{\vec{r}}\times\vec{L}_{\nu}) = - (m\cdot\dot{\vec{r}}\times\vec{r})\cdot \vec{L}_{\nu} = |\vec{L}_{\nu}|^2\tag{22}$$
erhält nach einigen Umformungen die folgende Relation
$$r\cdot \left(\frac{A}{G\cdot M_S\cdot m^2}\cdot\cos(\nu) + 1\right) = \frac{L_{\nu}^2}{G\cdot M_S\cdot m^2}\tag{23}$$
und das resultiert wiederum in die Kegelschnittsgleichung mit
$$\epsilon = \frac{|\vec{A}|}{G\cdot M_S\cdot m^2}\Rightarrow\epsilon\sim A\tag{24}$$
Vis Viva Satz
Schaut man sich die Situation im Perihel $q$ und im Aphel $Q$ an, so gilt gemäß der Drehimpulserhaltung:
$$\frac{L_{\nu}}{m} = |\vec{r}\times\dot{\vec{r}}| = q\cdot v_q = Q\cdot v_Q\tag{25}$$
Die Energiegleichungen an diesen beiden speziellen Bahnpunkten sind:
| \[\begin{split} E = \frac{1}{2}\cdot m\cdot v_q^2 - G\cdot \frac{M_S\cdot m}{q} & \Leftrightarrow E \cdot q^2 = \frac{1}{2}\cdot m\cdot v_q^2\cdot q^2 - G\cdot M_S\cdot m\cdot q \\ E = \frac{1}{2}\cdot m\cdot v_Q^2 - G\cdot \frac{M_S\cdot m}{Q} & \Leftrightarrow E \cdot Q^2 = \frac{1}{2}\cdot m\cdot v_Q^2\cdot Q^2 - G\cdot M_S\cdot m\cdot Q \end{split}\tag{26}\] |
Subtrahiert man beide Gleichungen unter Berücksichtigung der Relationen $q\cdot v_q$ = $Q\cdot v_Q$ und $q + Q = 2a$ voneinander, so hat man
$$E\cdot (Q^2 - q^2) = -G\cdot M_S\cdot m\cdot (Q - q)\Rightarrow E = -G\cdot\frac{M_S\cdot m}{2a}\tag{27}$$
Vergleicht man das Ergebnis mit der Gesamtenergie
$$- G\cdot \frac{M_S\cdot m}{2a} = \frac{1}{2}\cdot m\cdot v^2 - G\cdot \frac{M_S\cdot m}{r}\tag{28}$$
so erhält man den Vis-Viva Satz. Dieser ist zwar keine Erhaltungsgrösse, beruht aber auf der Gesamtenergie $E$.
\[\begin{align} \text{Ellipse:}\; v^2 &= G\cdot M_S\cdot\left(\dfrac{2}{r} - \dfrac{1}{a}\right) \\[2ex] \text{Parabel:}\; v^2 &= G\cdot M_S\cdot\dfrac{2}{r} \\[2ex] \text{Hyperbel:}\; v^2 &= G\cdot M_S\cdot\left(\dfrac{2}{r} + \dfrac{1}{a}\right) \end{align}\tag{29}\]
Diese gibt die momentane Geschwindigkeit $v = \dot{r}$ des Himmelskörpers auf seiner Bahn an. Für $r = a$ bekommt man die erste kosmische Geschwindigkeit $v_1$ (= Kreisbahngeschwindigkeit) und für $a = \infty$ die zweite kosmische Geschwindigkeit $v_2$ (= Fluchtgeschwindigkeit mit einem Parabelflug):
\[\begin{align} v_1 &= \sqrt{G\cdot \frac{M_S}{r}} \\[2ex] v_2 &= \sqrt{2\cdot G\cdot \frac{M_E}{r}} \\[2ex] v_3 &= \sqrt{2\cdot G\cdot \frac{M_S}{r}} \end{align}\tag{30}\]
$v_3$ wird als dritte kosmische Geschwindigkeit bezeichnet. Man verlässt dann antriebslos das Sonnensystem. Es bleibt nur noch zu sagen, dass der Runge-Lenz Vektor im englischen Sprachraum »Laplace-Vector« heißt und dass $\vec{L}_{\nu}\cdot\vec{R}_L = 0$ gilt. Sie stehen beide senkrecht aufeinander.
Baryzentrum
Ausgehend von den heliozentrisch-ekliptikalen Koordinaten aller acht Planeten und Pluto, transformiert man diese in die karthesischen Koordinaten. Mit der Gesamtmasse $\mu$, der Sonnenmasse M$_S$, den Planetenmassen $m_i$ und den reziproken Planetenmassen
| $$\mu = M_S + \sum_{i=1}^9 m_i = M_S\left(1 + \sum_{i=1}^9 \frac{m_i}{M_S}\right) = \sum_{i=0}^9 m_i \qquad\text{mit}\qquad m_0 = M_S$$ |
kann man nun nach der Summation der karthesischen Koordinaten die heliozentrisch-ekliptikalen Koordinaten des solaren Baryzentrums $\vec{G}(L,B,G)$ {heliozentrisch-ekliptikale Koordinaten} berechnen.
$$\vec{G}(L,B,G) = \frac{1}{\mu}\cdot \sum_{i=1}^9 m_i\cdot r_{B,i}\cdot \vec{e}(l_{B,i},b_{B,i})$$
oder ausgeschrieben:
| \[\begin{aligned} G\cdot \cos(B)\cdot\cos(L) = X = &\frac{1}{\mu}\cdot \sum_{i=1}^9 m_i\cdot r_{B,i}\cdot \cos(b_{B,i})\cdot \cos(l_{B,i}) \\ G\cdot \cos(B)\cdot \sin(L) = Y = &\frac{1}{\mu}\cdot \sum_{i=1}^9 m_i\cdot r_{B,i}\cdot \cos(b_{B,i})\cdot \sin(l_{B,i}) \\ G\cdot \sin(B) = Z = & \frac{1}{\mu}\cdot \sum_{i=1}^9 m_i\cdot r_{B,i}\cdot \sin(b_{B,i}) \end{aligned}\] |
Die Transformation von den heliozentrisch-ekliptikalen Koordinaten zu den baryzentrischen Koordinaten der Planeten erfolgt hier.
Periheldrehung
Dieses Thema bekam eine eigene Seite.
Raketengleichung
Dieses Thema bekam eine eigene Seite.
Kreisbahnsatelliten
Dieses Thema bekam eine eigene Seite.
Komet innerhalb der Erdbahn
Dieses Thema bekam eine eigene Seite.