Inhaltsverzeichnis
Die Raketengleichung
Aufgabe
Eine Rakete der Anfangsmasse $m_0$ stößt pro Zeiteinheit die Gasmenge $\alpha = \frac{\Delta m}{\Delta t} \gt 0$ mit der konstanten Geschwindigkeit $v_0$ aus. Gesucht ist die Bewegungsgleichung. Die Gravitationskraft soll dabei als konstant angenommen werden. Das bedeutet, dass das Raketenproblem nur in der näheren Umgebung der Erdoberfläche betrachtet werden soll.
Lösung
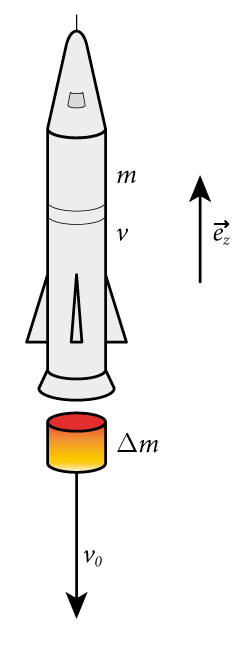
Die Rakete der Masse $m(t)$ bewegt sich mit der Geschwindigkeit $v(t)$ nach oben. Dabei wird die Masse $\Delta m$ mit der konstanten Geschwindigkeit $v_0$ (relativ zur Rakete) nach unten ausgestoßen. Für die Rakete muss das Newtonsche Kraftgesetz in seiner ursprünglichen Form
$$\vec{F} = \frac{\mathrm{d}\vec{p}}{\mathrm{d}t}\tag{1}$$
zu Grunde gelegt werden, weil die Raketenmasse veränderlich ist. Daher gilt
$$\frac{\mathrm{d}\vec{p}}{\mathrm{d}t} = m\cdot \frac{\mathrm{d}\vec{v}}{\mathrm{d}t} + \vec{v}\cdot \frac{\mathrm{d}m}{\mathrm{d}t}\tag{2}$$
wobei
$$\vec{v} = v\cdot \vec{e}_z\tag{3}$$
die vertikale Geschwindigkeit bedeutet. Die ausgestoßenen Gase tragen innerhalb des Zeitintervalls $\Delta t$ den Impuls
$$\Delta \vec{p}' = \Delta m\cdot (v - v_0)\cdot \vec{e}_z = \alpha\cdot (v - v_0)\cdot \Delta t\cdot \vec{e}_z\tag{4}$$
weg. Dies führt zu einer Kraft auf die Rakete (Rückstoßkraft) von der Größe
$$\vec{F}' = -\frac{\Delta\vec{p}'}{\Delta t} = - \alpha\cdot (v - v_0)\cdot \vec{e}_z\tag{5}$$
Außerdem wirkt die Schwerkraft zum Erdmittelpunkt mit $-m\cdot g\cdot \vec{e}_z$. Somit lautet das Newtonsche Kraftgesetz
\[\begin{aligned} m\cdot \frac{\mathrm{d}v}{\mathrm{d}t} + v\cdot \frac{\mathrm{d}m}{\mathrm{d}t} &= -\alpha\cdot (v-v_0) - m\cdot g \\ &= -m\cdot g - \frac{\mathrm{d}m}{\mathrm{d}t}\cdot (v-v_0) \end{aligned}\tag{6}\]
Diese Bilanz gilt im fest auf der Erde verankertem Inertialsystem. Mit $m = m_0\cdot \alpha\cdot t$ und $\frac{\mathrm{d}m}{\mathrm{d}t}= -\alpha$ folgt
$$m\cdot \frac{\mathrm{d}v}{\mathrm{d}t}\cdot \vec{e}_z = +\alpha\cdot v_0\cdot \vec{e}_z - m\cdot g\cdot \vec{e}_z\tag{7}$$
Das Glied $\alpha\cdot v_0$ auf der rechten Seite stellt die vom Rückstoß herrührende Kraft dar. Wir erhalten weiter
\[\begin{aligned} \int\limits_0^v \mathrm{d}v &=\int\limits_0^t\left(\frac{\alpha\cdot v_0}{m_0 - \alpha\cdot t}-g\right) \mathrm{d}t, \\ v(t) &= -g\cdot t + v_0\cdot \int\limits_0^t \frac{\frac{\alpha}{m_0}}{1 - \left(\frac{\alpha}{m_0}\right)\cdot t}\mathrm{d}t \\ &= -g\cdot t - v_0\cdot \left[\ln\left(1 - \frac{\alpha}{m_0}\cdot t \right)\right]_0^t \\ &= -g\cdot t - v_0\cdot \ln\left(1 - \frac{\alpha}{m_0}\cdot t \right) \end{aligned}\tag{8}\]
Offensichtlich hängt die Raketengeschwindigkeit linear von der Austrittsgeschwindigkeit $v_0$ der Rückstoßgase ab. Durch eine weitere Integration ergibt sich die Höhe $h(t)$ der Rakete mit
| $$h = \int\limits_0^h v\;\mathrm{d}t = -\frac{1}{2}\cdot g\cdot t^2 - v_0\cdot \int\limits_0^t \ln\left(1 - \frac{\alpha}{m_0}\cdot t \right) \mathrm{d}t\tag{9}$$ |
Mit der Substitution $u = 1 - \frac{\alpha}{m_0}\cdot t$ und $\mathrm{d}u = -(\frac{\alpha}{m_0})\mathrm{d}t$ folgt daraus
| \[\begin{aligned} \frac{v_0\cdot m_0}{\alpha}\cdot \int\limits_{t=0}^t \ln(u)\mathrm{d}u &= \frac{v_0\cdot m_0}{\alpha}\cdot\bigg[u\cdot \ln u - u\bigg]_{t=0}^t \\ &=\frac{v_0\cdot m_0}{\alpha}\cdot \left[\left(1-\frac{\alpha}{m_0}\cdot t\right)\cdot \ln\left(1-\frac{\alpha}{m_0}\cdot t\right) - \left(1-\frac{\alpha}{m_0}\cdot t\right)\right]_{t=0}^t \\ &= \frac{v_0\cdot m_0}{\alpha}\cdot\left[\left(1-\frac{\alpha}{m_0}\cdot t\right)\cdot \ln\left(1-\frac{\alpha}{m_0}\cdot t\right) + \frac{\alpha}{m_0}\cdot t\right] \end{aligned}\tag{10}\] |
Damit folgt für die Höhe der Rakete nach der Zeit $t$
| $$h = -\frac{1}{2}\cdot g\cdot t^2 + \frac{v_0\cdot m_0}{\alpha}\cdot \left(1-\frac{\alpha}{m_0}\cdot t\right)\cdot \ln\left(1-\frac{\alpha}{m_0}\cdot t\right) + v_0\cdot t\tag{11}$$ |
Um den Zeitpunkt des Brennschlusses $T$ zu bestimmen, führen wir als $m_1$ die Masse des Gehäuses der Rakete ein.
Es gilt dann: $m_0 = m_1 + \alpha\cdot T$, wobei $\alpha\cdot T$ die Brennstoffmasse ist.
$$T = \frac{m_0 - m_1}{\alpha}\tag{12}$$
Zur Zeit des Brennschlusses hat die Rakete die Geschwindigkeit
| $$v_1 = v(T) = -g\cdot \frac{m_0 - m_1}{\alpha} - v_0\cdot \ln\left(\frac{m_1}{m_0}\right) = -g\cdot \frac{m_0 - m_1}{\alpha} + v_0\cdot\ln\left(\frac{m_0}{m_1}\right)\tag{13}$$ |
am Ort
| $$h_1 = h(T) = -\frac{1}{2}\cdot g\cdot\left(\frac{m_0 - m_1}{\alpha}\right)^2 + v_0\cdot \left[\frac{m_0 - m_1}{\alpha} + \frac{m_1}{\alpha}\cdot \ln\left(\frac{m_1}{m_0} \right)\right]\tag{14}$$ |
Die Endgeschwindigkeit der Rakete hängt linear von der Austrittsgeschwindigkeit $v_0$ der Rückstoßgase ab und ist proportional dem Logarithmus des Verhältnisses aus Anfangs- und Endmasse. Für die weitere Bewegung der Rakete folgt nach dem Energiesatz
$$\frac{1}{2}\cdot m\cdot v_1^2 = m\cdot g\cdot h_2\tag{15}$$
Daraus lässt sich die Höhe $h_2$, die die Rakete nach Brennschluss erreicht, berechnen mit
$$h_2 = \frac{v_1^2}{2\cdot g}\tag{16}$$
Die gesamte Steighöhe der Rakete ist dann
| \[\begin{aligned} h =& h_1 + h_2 = h_1 + \frac{v_1^2}{2\cdot g} \\ h =& \frac{1}{2}\cdot g\cdot \left(\frac{m_0-m_1}{\alpha}\right)^2 - \frac{1}{2}\cdot g\cdot \left(\frac{m_0-m_1}{\alpha}\right)^2 \\ +& v_0\cdot \left(\frac{m_0-m_1}{\alpha}\right)\cdot \ln\left(\frac{m_1}{m_0}\right) \\ +& \frac{v_0^2}{2\cdot g}\cdot \ln^2\left(\frac{m_1}{m_0}\right) \\ +& v_0\cdot \left(\frac{m_0-m_1}{\alpha}\right) \\ +& v_0\cdot \frac{m_1}{\alpha}\cdot \ln\left(\frac{m_1}{m_0} \right) \end{aligned}\tag{17}\] |
Man erhält schließlich
\[\begin{aligned} h &= \left(\ln\frac{m_1}{m_0}+1\right)\cdot v_0\cdot \left(\frac{m_0-m_1}{\alpha}\right) \\ &+ v_0\cdot \ln\frac{m_1}{m_0}\cdot\left(\frac{v_0}{2\cdot g}\cdot \ln\frac{m_1}{m_0} + \frac{m_1}{\alpha}\right) \end{aligned}\tag{18}\]