Inhaltsverzeichnis
Koordinatenreduktion
Dieses Kapitel befasst sich mit der Korrektur von Koordinaten, die durch spezielle himmelsmechanische, atmosphärische und relativistische Phänomene und Effekte auftreten. Nachstehend gilt für julianische Jahrhunderte $T$ bezüglich der Epoche $J2000$:
$$T = \frac{JDE - 2451545.0}{36525}\tag{1}$$
Präzession
In der Astronomie ist mit der Präzession eine Richtungsänderung der Erdachse gemeint, die durch die Anziehung des Mondes und der Sonne in Verbindung mit der Abplattung auftritt. Sie äußert sich durch das Fortschreiten des Frühlingspunkts entlang der Ekliptik, woraus sich auch die Bezeichnung Präzession (lateinisch für ‚Fortschreiten‘) herleitet. Die Präzessionsgleichungen beruhen auf O. Montenbruck. Zuerst werden einige Hilfswinkel benötigt; diese müssen vorab in Grad umgerechnet werden.
| Tabelle 1 | ||
|---|---|---|
| Winkel | von | bis |
| $\Psi$ | $1$ | |
| $\chi$ | $1$ | |
| $90^\circ + z$ | | $3$ |
| $90^\circ - \zeta$ | | $3$ |
| $\Lambda$ | | $2$ |
| Tabelle 2: Äquator |
|---|
| \[ \begin{align} \zeta =&\; 2306\overset{''}{.}2181\cdot T + 0\overset{''}{.}30188\cdot T^2 + 0\overset{''}{.}017998\cdot T^3\\ z =&\; 2306\overset{''}{.}2181\cdot T + 1\overset{''}{.}09468\cdot T^2 + 0\overset{''}{.}018203\cdot T^3\\ \theta =&\; 2004\overset{''}{.}3109\cdot T - 0\overset{''}{.}42665\cdot T^2 - 0\overset{''}{.}041833\cdot T^3\\ \chi =&\; 10\overset{''}{.}5526\cdot T - 2\overset{''}{.}38064\cdot T^2 - 1\overset{''}{.}125\cdot 10^{-3}\cdot T^3 \end{align} \] |
$$\alpha' = \alpha + \zeta + z + \theta\cdot\tan(\delta)\cdot\sin(\alpha)\tag{2}$$ $$\delta' = \delta + \theta\cdot\cos(\alpha)\tag{3}$$
| Tabelle 3: Ekliptik |
|---|
| \[ \begin{align} \Pi =&\; 629554\overset{''}{.}982 - 869\overset{''}{.}8089\cdot T + 0\overset{''}{.}03536\cdot T^2\\ p =&\; 5029\overset{''}{.}0966\cdot T + 1\overset{''}{.}11113\cdot T^2 - 6\overset{''}{.}0\cdot 10^{-6}\cdot T^3\\ \eta =&\; 47\overset{''}{.}0029\cdot T - 0\overset{''}{.}03302\cdot T^2 - 6\overset{''}{.}0\cdot 10^{-5}\cdot T^3\\ \psi =&\; 5038\overset{''}{.}7784\cdot T - 1\overset{''}{.}07259\cdot T^2 - 1\overset{''}{.}147\cdot 10^{-3}\cdot T^3\\ \end{align} \] |
$$\lambda' = \lambda + p + \eta\cdot\tan(\beta)\cdot\cos(\lambda - \Pi)\tag{4}$$ $$\beta' = \beta - \eta\cdot\sin(\lambda - \Pi)\tag{5}$$
$$i' = i - \eta\cdot\cos(\Pi - \Omega)\tag{6}$$ $$\Omega' = \Omega + p - \eta\frac{\sin(\Pi - \Omega)}{\tan(i)} \quad \forall i \neq 0^{\circ}\tag{7}$$ $$\omega' = \omega + \eta\frac{\sin(\Pi - \Omega)}{\sin(i)}\tag{8}$$
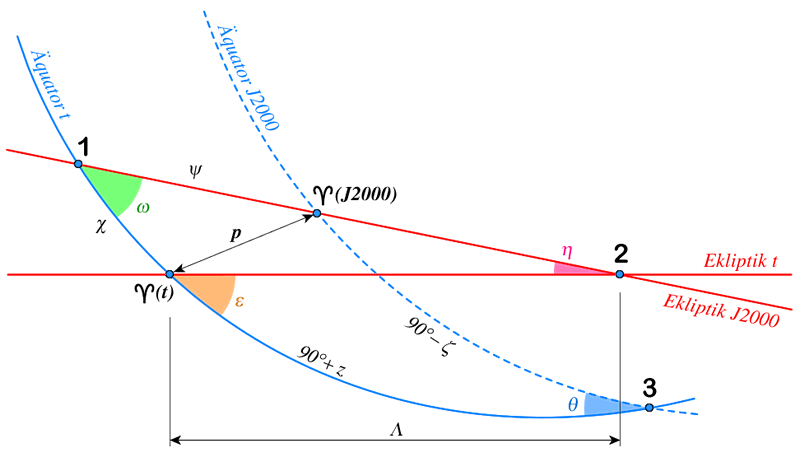
![]() $(t)$ = Frühlingspunkt zur Epoche des Datums
$(t)$ = Frühlingspunkt zur Epoche des Datums
![]() $(J2000)$ = Frühlingspunkt zur Standard-Epoche $J2000$
$(J2000)$ = Frühlingspunkt zur Standard-Epoche $J2000$
Ekliptik $t$ = Ekliptik zur Epoche des Datums
Ekliptik $J2000$ = Ekliptik zur Standard-Epoche $J2000$
Äquator $t$ = Äquator zur Epoche des Datums
Äquator $J2000$ = Äquator zur Standard-Epoche $J2000$
$p$ = Längendifferenz zwischen dem alten Frühlingspunkt und dem neuen Frühlingspunkt
$\Lambda$ = p + $\Pi$
$\Pi$ = Längendifferenz zwischen den Schnittpunkten von Ekliptik 2000.0/Äquator 2000.0 und Ekliptik 2000.0/Ekliptik t
$\varepsilon$ = Ekliptikschiefe
$\chi$ = Längendifferenz zwischen den Schnittpunkten von Ekliptik 2000.0/Äquator t und Ekliptik t/Äquator t (aktueller Frühlingspunkt)
$z$ = Längendifferenz zwischen den Schnittpunkten von Äquator t/Ekliptik t (aktueller Frühlingspunkt) und Äquator 2000.0/Äquator t
$\zeta$ = Längendifferenz zwischen den Schnittpunkten von Ekliptik 2000.0/Äquator 2000.0
$\alpha, \delta$ = alte, äquatoriale Koordinaten
$\alpha', \delta'$ = neue, präzessionskorrigierte, äquatoriale Koordinaten
$\lambda, \beta$ = alte, ekliptikale Koordinaten
$\lambda', \beta'$ = neue, präzessionskorrigierte, ekliptikale Koordinaten
$i,\Omega,\omega$ = alte Bahnlageelemente
$i',\Omega',\omega'$ = neue, präzessionskorrigierte Bahnlageelemente
Nutation
Die astronomische Nutation (lat.: nutare ‚nicken‘) ist der schwankende Teil der Präzession der Erdachse im Raum unter dem Einfluss von Sonne und Mond. Die Stärke dieser Schwankungen wird durch die Präzession der Mondbahn verursacht, deren Knotenlinie mit einer Periode von $18.6$ Jahren die Erde umläuft. Die zur Berechnung der Nutation benötigten Mittelwerte lauten:
| Tabelle 4 | |
|---|---|
| Mond | Sonne |
| \begin{align} m =\;& 134\overset{\circ}{.}96298139 \\ &+ 477198\overset{\circ}{.}86739806 \cdot T \\ &+ 0\overset{\circ}{.}00869722 \cdot T^2\\ \end{align} | \begin{align} M =\;&357\overset{\circ}{.}52772333 \\ &+35999\overset{\circ}{.}05034 \cdot T \\ &-0\overset{\circ}{.}000160278 \cdot T^2\\ \end{align} |
| \begin{align} l =\;& 218\overset{\circ}{.}31643250 \\ &+ 481267\overset{\circ}{.}88127722 \cdot T \\ &+ 0\overset{\circ}{.}00161167 \cdot T^2\\ \end{align} | \begin{align} L =\;&280\overset{\circ}{.}46606944 \\ &+36000\overset{\circ}{.}76979722 \cdot T \\ &+0\overset{\circ}{.}0003025 \cdot T^2\\ \end{align} |
| \begin{align} \Omega =\;&125\overset{\circ}{.}04452222 \\ &-1934\overset{\circ}{.}13626083 \cdot T \\ &+0\overset{\circ}{.}00207083 \cdot T^2\\ \end{align} | |
| Tabelle 5 | ||
|---|---|---|
| Korrekturwert | O. Montenbruck: | J. Meeus: |
| $\Delta\lambda$ | $-17\overset{''}{.}200\cdot \sin(\Omega) + 0\overset{''}{.}206\cdot \sin(2 \Omega)$ | $-17\overset{''}{.}2327\cdot \sin(\Omega) + 0\overset{''}{.}2088\cdot \sin(2 \Omega)$ |
| $-1\overset{''}{.}319\cdot \sin(2 L) + 0\overset{''}{.}143\cdot \sin(M)$ | $-1\overset{''}{.}2729\cdot \sin(2 L) +0\overset{''}{.}1261 \sin(M)$ | |
| $-0\overset{''}{.}227\cdot \sin(2 l) +0\overset{''}{.}071\cdot \sin(m)$ | $-0\overset{''}{.}2037\cdot \sin(2 l) +0\overset{''}{.}0675\cdot \sin(m)$ | |
| $\Delta\varepsilon$ | $+9\overset{''}{.}203\cdot \cos(\Omega) - 0\overset{''}{.}090\cdot \cos(2 \Omega)$ | $+9\overset{''}{.}2100\cdot \cos(\Omega) - 0\overset{''}{.}0904\cdot \cos(2 \Omega)$ |
| $+0\overset{''}{.}574\cdot \cos(2 L) + 0\overset{''}{.}022\cdot \cos(2 L + M)$ | $+0\overset{''}{.}5522\cdot \cos(2 L) +0\overset{''}{.}0216\cdot \cos(2 L + M)$ | |
| $+0\overset{''}{.}098\cdot \cos(2 l) + 0\overset{''}{.}020\cdot \cos(2 l -\Omega)$ | $+0\overset{''}{.}0884\cdot \cos(2 l) +0\overset{''}{.}0183\cdot \cos(2 l -\Omega)$ | |
Es gilt:
$$\lambda' = \lambda + \frac{\Delta\lambda}{3600\tfrac{''}{^\circ}}\tag{9}$$ $$\varepsilon' = \varepsilon + \frac{\Delta\varepsilon}{3600\tfrac{''}{^\circ}}\tag{10}$$
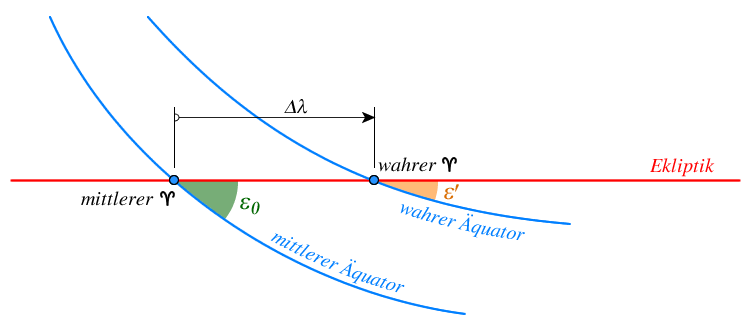
mittlerer ![]() = vor der Korrektur
= vor der Korrektur
wahrer ![]() = nach der Korrektur
= nach der Korrektur
$\varepsilon$ = alte Ekliptikschiefe
$\varepsilon '$ = neue, nutationskorrigierte Ekliptikschiefe
$\lambda$ = alte ekliptikale Länge
$\lambda '$ = neue, nutationskorrigierte ekliptikale Länge
$\Delta\lambda$ = Längendifferenz zwischen alter und neuer, nutationskorrigierter Länge
Beispiel
 Man berechne die Nutationskorrekturen in Länge $\Delta \lambda$ und in Schiefe $\Delta \varepsilon$ für den Zeitpunkt 21.5.2023, 10:15 MESZ.
Man berechne die Nutationskorrekturen in Länge $\Delta \lambda$ und in Schiefe $\Delta \varepsilon$ für den Zeitpunkt 21.5.2023, 10:15 MESZ.
Für den gegebenen Zeitpunkt wurde der julianische Tag bereits in diesem Beispiel berechnet zu $JD = 2460085.84375$. Für das Jahr 2023 beträgt der Wert von $\Delta T$ zirka $\Delta T = 69^{s}$. Für die Umrechnung in die Zeitskala der dynamischen Zeit $TD$ rechnet man
\(\begin{align} JDE &= JD + \frac{\Delta T}{86400}\\ &= 2460085.84375 + \frac{69^{s}}{86400\tfrac{s}{d}}\\ &= 2460085.844548611 \end{align}\)
Damit erhält man die julianischen Jahrhunderte $T$ bezüglich der Epoche $J2000$ mit
\(\begin{align} T&= \frac{JD - 2451545.0}{36525}\\ &= \frac{2460085.844548611 - 2451545.0}{36525}\\ &= 0.23383557970187463 \end{align}\)
Nun ermittelt man die Grundwinkel für Mond $m, l, \Omega$ und Sonne $M, L$ aus den oben stehenden Gleichungen sukzessive mit
| Mond | Sonne |
|---|---|
| \(\begin{align} m &= 111721\overset{\circ}{.}03724804732\\ &= 121\overset{\circ}{.}037248\\ l &= 112755\overset{\circ}{.}87053097668\\ &= 75\overset{\circ}{.}870531\\ \Omega &= -327\overset{\circ}{.}22523832089837\\ &= 32\overset{\circ}{.}774762 \end{align}\) | \(\begin{align} M &= 8775\overset{\circ}{.}386519540358\\ &= 135\overset{\circ}{.}38652\\ L &= 8698\overset{\circ}{.}726961232065\\ &= 58\overset{\circ}{.}726961 \end{align}\) |
Für große Winkel wurde hier die Reduktions-Funktion verwendet, um die Winkel in das Intervall [0°-360°] zu bringen.
Nun kann man entweder die Gleichungen von O. Montenbruck oder von J. Meeus verwenden, um $\Delta\lambda$ und $\Delta\varepsilon$ zu berechnen, man erhält:
| Montenbruck | Meeus | |
|---|---|---|
| $\Delta\lambda =$ | $-10\overset{''}{.}240$ | $-10\overset{''}{.}218$ |
| $\Delta\varepsilon =$ | $+7\overset{''}{.}334$ | $+7\overset{''}{.}359$ |
Die nutationskorrigierten Größen $\lambda'$ und $\varepsilon'$ erhält man nun durch Addition gemäß den obigen Beziehungen
\(\begin{align} \lambda' &= \lambda + \frac{\Delta\lambda}{3600\tfrac{''}{^\circ}}\\ \varepsilon' &= \varepsilon + \frac{\Delta\varepsilon}{3600\tfrac{''}{^\circ}} \end{align}\)
Eine Illustration der genaueren Berechnung der Nutation findet man in diesem Abschnitt.
Aberration
Die Aberration (lat. aberratio: Verirrung) beschreibt die scheinbare Position eines Himmelsobjekts durch einen bewegten Beobachter, auch bedingt durch die Endlichkeit der Lichtgeschwindigkeit $c$. Der Ort des Sterns oder Planeten erscheint verschoben und muss korrigiert werden.
Die Konstanten:
Nimmt man die Erdbahngeschwindigkeit $v_1 = 29.785 \frac{km}{s}$ und die Äquatorgeschwindigkeit $v_2 = 465.096 \frac{m}{s}$, so erhält man die 1. Aberrationskonstante $k_1$ bzw. 2. Aberrationskonstante $k_2$:
$$k_1 = \dfrac{20\overset{''}{.}4934472502}{3600''}\tag{11}$$ $$k_2 = \dfrac{0\overset{''}{.}3200138652125}{3600''}\tag{12}$$
Die tägliche Aberration:
Die tägliche Aberration ist die Abweichung durch die Erdrotation.
\[\begin{align} A_t &= k_2\cdot \frac{\cos(\beta_0) \cdot \cos(\theta - \alpha)}{15^h \cos(\delta)}\\ D_t &= k_2\cdot \cos(\beta_0) \cdot \sin(\theta - \alpha) \cdot \sin(\delta) \end{align}\tag{13}\]
Die neuen scheinbaren, äquatorialen Koordinaten bekommt man durch Addition: $$\alpha_t = \alpha_i - A_t \quad und \quad \delta_t = \delta_i - D_t\tag{14}$$
Die jährliche Aberration:
Die jährliche Aberration ist die Abweichung durch den Umlauf der Erde um die Sonne: \[\begin{align} A &= k_1\cdot \frac{\sin(L) \cdot \sin(\alpha) + \cos(L) \cdot \cos(\alpha) \cdot \cos(\varepsilon)}{15^h \cos(\delta)} \\\\ D &= k_1\cdot (\sin(\delta) \cdot \cos(\alpha) \cdot \sin(L)\\ &+ (\sin(\varepsilon) \cdot \cos(\delta)\\ &- \cos(\varepsilon) \cdot \sin(\delta) \cdot \sin(\alpha)) \cdot \cos(L)) \\\\ A_e &= k_1\cdot \epsilon \frac{\sin(\varpi) \cdot \sin(\alpha) + \cos(\varpi) \cdot \cos(\alpha) \cdot \cos(\varepsilon)}{15^h \cos(\delta)} \\\\ D_e &= k_1\cdot \epsilon (\sin(\delta) \cdot \cos(\alpha) \cdot \sin(\varpi)\\ &+ (\sin(\varepsilon) \cdot \cos(\delta)\\ &- \cos(\varepsilon) \sin(\delta) \cdot \sin(\alpha)) \cdot \cos(\varpi)) \end{align}\tag{15}\]
Die neuen scheinbaren, äquatorialen Koordinaten bekommt man wieder durch eine Addition:
$$\alpha_i = \alpha - (A + A_e) \quad und \quad \delta_i = \delta - (D + D_e)\tag{16}$$
$A_e$, A, $D_e$, D = Korrektur der jährlichen Aberration
$A_t$, $D_t$ = Korrektur der täglichen Aberration
$\theta$ = lokale Sternzeit des Beobachters
$\varpi$ = Perihellänge der scheinbaren Sonnenbahn (i.e. der Erde)
L = geozentrisch ekliptikale Länge des Planeten
$\epsilon$ = numerische Exzentrizität der Erdbahn
$\alpha$, $\delta$ = ungestörte, äquatoriale Koordinaten des Planeten
Abplattung
Die Thematik der Abplattung wird aufgrund des umfangreichen Inhalts in einem eigenen Kapitel illustriert.
Refraktion
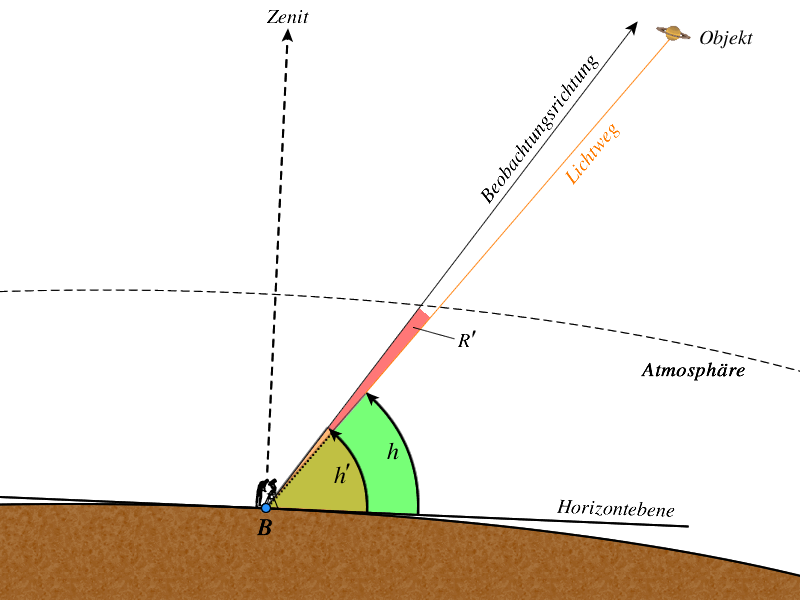
Die Refraktion ist die Richtungsänderung eines Lichtstrahls auf seinen Weg durch die geschichtete Atmosphäre. Ursache ist der Anstieg des Brechungsindexes. Sie bewirkt eine Anhebung des Himmelsobjekts in der Höhe. Es werden die Formeln angegeben, mit denen man aus der »luftlosen«, wahren Höhe $h$ mittels einer Addition der Refraktion $R(h)$ die scheinbare Höhe $h'$ berechnet werden kann. J. Meeus stellt in seinen Astronomical Algorithms eine Zahlenwert-Gleichung von G.G. Bennet vor, die das berechnt:
$$R(h) = \frac{1}{\tan\left(h + \dfrac{7\overset{\circ}{.}31}{h + 4\overset{\circ}{.}4}\right)}\tag{17}$$
Dabei ist $h$ in Grad einzusetzen, das Ergebnis erhält man in Bogenminuten. Die Gleichung versagt jedoch im Zenit ($h = 90^\circ$):
- $R(90^{\circ}) = -0\overset{'}{.}0013515$, statt Null. Das wird durch Addition von $C = +0\overset{'}{.}0013515$ zur rechten Seite von $R$ bewerkstelligt
(Für alle anderen Höhen gilt $C = 0'$. - Laut Bennet ist die Gleichung für alle Höhen $h$ gültig mit einem maximalen Fehler von $0\overset{'}{.}07$, der ca. bei $h \approx 12^{\circ}$ auftritt.
 Abb. 6: Refraktion R(h) nach Bennet
Abb. 6: Refraktion R(h) nach Bennet
Auch für das umgekehrte Problem gibt es eine einfache Näherungsformel, wenn man aus der scheinbaren Höhe $h'$ die Refraktion ermitteln möchte:
$$R(h') = \frac{1.02}{\tan\left(h' + \dfrac{10\overset{\circ}{.}3}{h' + 5\overset{\circ}{.}11}\right)}\tag{18}$$
- Für $h' = 90^{\circ}$ ist auch hier die Refraktion $R(h')\ne 0$, was mit dem Korrekturfaktor $+0\overset{'}{.}0019279$ beseitigt werden kann.
- Die Formel stammt von Sæmundsson und ist konsistent zu Bennets Gleichung, mit einer Differenz von $4''$.
Der nächste Punkt ist eine weitere Korrektur $K$ (in Bogenminuten) des Refraktionsverlaufs für alle Höhen, bis auf den Zenit mit:
$$K = - 0.06\cdot \sin(14.7\cdot R(h) + 13.0)\tag{19}$$
Als Letztes wird noch der Druck $p$ in [hPa] und die Temperatur $T$ in [°C] berücksichtigt. Sind die obigen Berechnungen abgeschlossen, so muss noch der Wetterterm $W$ multipliziert werden:
$$W(p,T) = \frac{p}{1013.246 \ \textsf{hPa}} \cdot \frac{283.16 \ K}{273.16 \ K + T}\tag{20}$$
Es gilt:
$$R(h) = W(p,T)\cdot\big{(}R(h) + C + K\big{)}\tag{21}$$
Die nachfolgende Tabelle stammt aus G.D. Roth (Handbuch für Sternfreunde) und zeigt die zu erwartenden Ablenkungen $R$ bei verschiedenen Temperaturen $T$ für $p = 1013.246 \textsf{hPa}$.
| Tabelle 6 | |||||
|---|---|---|---|---|---|
| Zenitdistanz | Refraktion $R$ | Refraktion $R$ | Zenitdistanz | Refraktion $R$ | Refraktion $R$ |
| $z$ | $T$ (10°C) | $T$ (0°C) | $z$ | $T$ (10°C) | $T$ (0°C) |
| $00^\circ 00'$ | $0' 00''$ | $0' 00''$ | $83^\circ 00'$ | $7' 24''$ | |
| $10^\circ 00'$ | $0' 10''$ | $0' 11''$ | $84^\circ 00'$ | $8' 28''$ | |
| $20^\circ 00'$ | $0' 21''$ | $0' 22''$ | $85^\circ 00'$ | $9' 52''$ | $10' 15''$ |
| $30^\circ 00'$ | $0' 34''$ | $0' 35''$ | $86^\circ 00'$ | $11' 45''$ | |
| $40^\circ 00'$ | $0' 49''$ | $0' 51''$ | $86^\circ 30'$ | $12' 56''$ | |
| $50^\circ 00'$ | $1' 09''$ | $1' 11''$ | $87^\circ 00'$ | $14' 22''$ | |
| $55^\circ 00'$ | $1' 23''$ | $87^\circ 30'$ | $16' 09''$ | ||
| $60^\circ 00'$ | $1' 41''$ | $1' 45''$ | $88^\circ 00'$ | $18' 18''$ | $19' 07''$ |
| $65^\circ 00'$ | $2' 04''$ | $88^\circ 30'$ | $21' 05''$ | ||
| $70^\circ 00'$ | $2' 39''$ | $2' 45''$ | $89^\circ 00'$ | $24' 37''$ | $25' 36''$ |
| $75^\circ 00'$ | $3' 34''$ | $3' 42''$ | $89^\circ 20'$ | $27' 36''$ | |
| $80^\circ 00'$ | $5' 19''$ | $5' 31''$ | $89^\circ 40'$ | $31' 09''$ | |
| $81^\circ 00'$ | $5' 52''$ | $90^\circ 00'$ | $35' 24''$ | $36' 38''$ | |
| $82^\circ 00'$ | $6' 33''$ | ||||
Die Höhe $h$ wird dann korrigiert mit
$$h' = h + \frac{R(h)}{60'}\tag{22}$$
$h$ = Höhe ohne Atmosphäre (wahre Höhe)
$h'$ = korrigierte Höhe (scheinbare Höhe)
$W$ = Wetterterm
$K$ = Korrekturterm
$R$ = Refraktion in Bogenminuten
Lichtlaufzeit
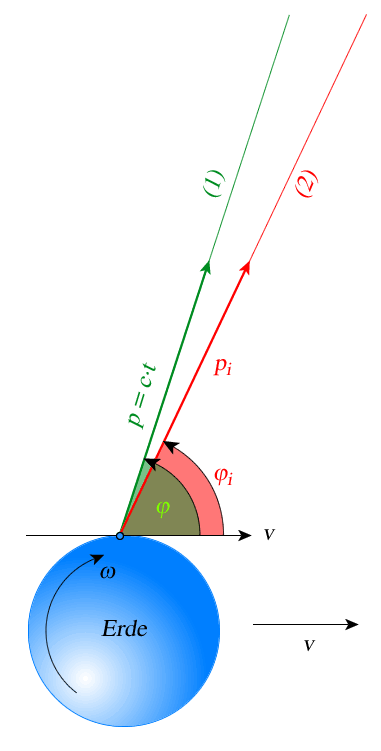
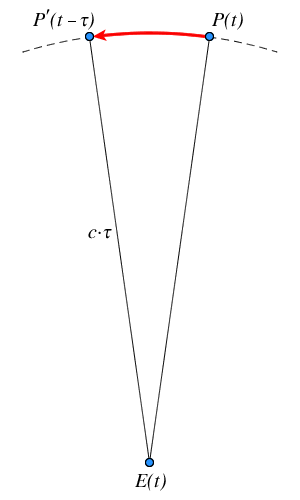
Das beobachtete Licht des Himmelsobjekts braucht zur Erde eine einige Minuten, bis zu einigen Stunden. Weil sich der Himmelskörper während dieser Zeit fortbewegt, befindet sich die beobachtete Position ein wenig hinter dem tatsächlich berechneten Ort zurück. Da die Lichtgeschwindigkeit $c$ erheblich größer ist als die Bewegung des beobachteten Objekts, liegt die Korrektur nur im Bereich von einigen Bogensekunden bis zu einer Bogenminute. Daher reicht hier die Näherung aus.
Der Beobachter $E$ hat zum Zeitpunkt $t$ den Eindruck, Licht von $P$ zu empfangen. Er erhält jedoch tatsächlich ein Signal, welches zum Zeitpunkt $t − \tau$ von $P'$ ausgesandt wurde. In der Zeit $\tau$ hat sich das Objekt auf der (als gekrümmt dargestellten) Bahn weiterbewegt.
\[\begin{align} \tau &= \frac{1 AE}{1c\cdot 24^h\cdot 3600^s} \cdot \Delta \text{ Tage}\\ &= 0\overset{d}{.}005775518304 \cdot \Delta\\ &\approx \frac{\Delta}{173.14} \text{ Tage} \end{align}\tag{23}\]
Die Korrektur der Lichtlaufzeit $\tau$ liefert die astrometrischen Koordinaten.
$\Delta$ = geozentrische Entfernung des Objekts.
$\tau$ = Lichtlaufzeit in Tagen
$c$ = Lichtgeschwindigkeit im Vakuum
Extinktion
Als Extinktion wird die Abschwächung des Lichts während seines Durchlaufs durch die Atmosphäre bezeichnet. Die folgenden Gleichungen stammen aus G.D. Roth (Handbuch für Sternfreunde). Der Luftmassenfaktor $M$ reduziert das einfallende Licht auf gleichlange Wege und bezeichnet gleichzeitig die Dicke der Luftmasse. Der Luftmassenfaktor M(z):
$$M(z) = \frac{1}{\cos(z - \Delta(z))}\tag{24}$$
mit
$$\Delta(z) \approx 0.05^{\circ}\cdot \frac{z}{93^{\circ} - z} \quad (0^{\circ} \leq z \leq 87^{\circ})\tag{25}$$
Im Zenit ist $M = 1$. Die Koeffizienten der Dunstextinktion $k_d$ und der Rayleigh - Streuung $k_r$ lauten:
$$k_r = \frac{0.00906\;p}{1013.25\;\textsf{hPa}}\cdot \left(\frac{\lambda}{1 \textsf{µm}}\right)^{-4}\tag{26}$$ $$k_d = 1.086\cdot \beta\cdot \left(\frac{\lambda}{1 \textsf{µm}}\right)^{-\alpha}\tag{27}$$
$\alpha$ ist hier der Wellenlängenexponent. Normalerweise ($\beta$ = 0.1) ist $\alpha = 1.3$, bei Staubstürmen ist $\alpha = 0.5$. Bei Wolken ist $\alpha = 0$ und $\beta$ sehr hoch. $\lambda$ ist die beobachtete Wellenlänge. Gelbes Licht: $\lambda = 550\;nm$. Im Zenit ist die Lichtausbeute $\mu (z) = 1$. Im Allgemeinen gilt deshalb $\beta\approx$ 0.1.
Es gilt $k_r$ + $k_d = 0.335252293177$. Das Licht eines Sterns im Zenit ist schon leicht geschwächt. Zur Ermittelung der Lichtausbeute wird deshalb der bereits angedeutete Faktor $\beta$ eingeführt, der den Zustand der Atmosphäre charakterisiert:
- $\beta = 0.05$: Himmel absolut klar.
- $\beta = 0.10$: Himmel leicht getrübt.
- $\beta = 0.20$: Himmel stark getrübt.
Als nächstes wird die optische Durchlässigkeit $T$ (Opazität) mit Hilfe von $M$ gebraucht. Sie gibt die Abschwächung des Lichts an.
$$m(z) = (k_r + k_d)\cdot M(z)\tag{28}$$ $$T(z) = 10^{-0.4 \cdot m(z)}\tag{29}$$
Die Extinktion $E$ ist dann die gewünschte Korrektur der Helligkeit des Himmelobjekts.
$$E(z) = (k_r + k_d + D(\lambda)\cdot t)\cdot (M(z) - 1)\tag{30}$$ $$\mu(z) = 10^{-0.4\cdot E(z)}\tag{31}$$
Der Term $D(\lambda)$ ist der Driftkoeffizient und kann je nach meteorologischen Bedingungen 0.001 $\tfrac{mag}{h}$ bis 0.1 $\tfrac{mag}{h}$ betragen. $E$ muss dann nur noch zur Größenklasse des Stern addiert werden. t ist die Zeit in Stunden, in der sich der Koeffizient D ändert. Die Extinktionstabelle stammt von der Sternwarte Höfingen.
| Tabelle 7 | |||||||
|---|---|---|---|---|---|---|---|
| $z[^\circ]$ | $E(z)$ | $z[^\circ]$ | $E(z)$ | $z[^\circ]$ | $E(z)$ | $z[^\circ]$ | $E(z)$ |
| $0 $ | $0\overset{^{m}}{.}0 $ | $50$ | $0\overset{^{m}}{.}12$ | $76$ | $0\overset{^{m}}{.}71$ | $82$ | $1\overset{^{m}}{.}18$ |
| $20$ | $0\overset{^{m}}{.}01$ | $60$ | $0\overset{^{m}}{.}23$ | $77$ | $0\overset{^{m}}{.}77$ | $84$ | $1\overset{^{m}}{.}49$ |
| $30$ | $0\overset{^{m}}{.}03$ | $70$ | $0\overset{^{m}}{.}45$ | $78$ | $0\overset{^{m}}{.}83$ | $86$ | $2\overset{^{m}}{.}04$ |
| $40$ | $0\overset{^{m}}{.}06$ | $74$ | $0\overset{^{m}}{.}60$ | $80$ | $0\overset{^{m}}{.}99$ | $88$ | $3\overset{^{m}}{.}10$ |
$z$ = Zenitdistanz = $90^{\circ}-h$
$m(z)$ = Transmissionsexponent
$M(z)$ = Luftmassenfaktor
$\Delta (z)$ = Hilfswert
$k_r$ = Zenitextinktion
$k_d$ = Dunstextinktion
$\lambda$ = Wellenlänge
$\alpha$ = Wellenlängenexponent
$T(z)$ = Transmission oder Opazität
$\mu (z)$ = Lichtausbeute
$E(z)$ = Extinktion in Größenklassen (mag)
$p$ = Luftdruck
$β$ = Zustandsfaktor der Atmosphäre
$t$ = Zeit
Reihenfolge der Korrekturen
Es muss eine bestimmte Reihenfolge eingehalten werden (Expl. Suppl.):
| Tabelle 8 | |
|---|---|
| 1. Lichtlaufzeit | Parallaxe |
| 2. Aberration | Abplattung |
| 3. Präzession | Refraktion |
| 4. Nutation | Extinktion |
Die Lichtlaufzeit erfolgt als erstes, dann Aberration, Präzession und zum Schluss die Nutation. Bei der Parallaxe, Abplattung, Refraktion und Extinktion ist die Reihenfolge unwichtig.
Obwohl die Begriffe im Astronomie Lexikon erwähnt werden, sind sie hier nochmal zusammengefasst mit einer Tabelle zur besseren Übersicht wiedergegeben.
Die geometrische Position
Die geometrischen Koordinaten eines Planeten ist die wahre Position eines Himmelskörpers zu einem gegebenen Zeitpunkt. Das heißt, dass die Aberration und Lichtlaufzeit nicht berücksichtigt wurde. Es handelt sich um die mittleren Bahnelemente und die heliozentrischen Koordinaten, die nur störungstheoretische Korrekturen erfahren haben. Sowie daraus durch Koordinatentransformation erzeugte geozentrische Koordinaten, sei es ekliptikal oder äquatorial.
Die astrometrische Position
Es handelt sich hier um die ekliptikalen oder äquatorialen Koordinaten, die durch die Lichtlaufzeit korrigiert wurden und deshalb in temporäre Sternkarten eingetragen werden können, wenn die Sternpositionen durch die Parallaxe und die Eigenbewegungen ebenfalls korrigiert wurden.
Die scheinbare Position
Das sind tatsächlich ursprünglich geo- oder astrometrische Koordinaten, die durch die Korrekturen wie Aberration, Refraktion und die Parallaxe berechnet werden und die wirkliche Position am Himmel wiedergeben, wie sie von einem Beobachter gesehen wird.
Die wahre Position
Werden Koordinaten mit mittleren Äquinoktium durch die Nutation korrigiert, so erhält man die wahren, ekliptikalen Koordinaten.
Tabelle
| Tabelle 9: Bezeichung der Koordinaten nach ihren Korrekturen | |||||
|---|---|---|---|---|---|
| Korrektur | geometrische | astrometrische | scheinbare | wahre | geodätische |
| Lichtlaufzeit | ✅ | ||||
| Aberration | ✅ | ||||
| Präzession | ✅ | ||||
| Nutation | ✅ | ||||
| Parallaxe | ✅ | ||||
| Refraktion | ✅ | ||||
| Abplattung | ✅ | ||||