Inhaltsverzeichnis
Kegelschnitte
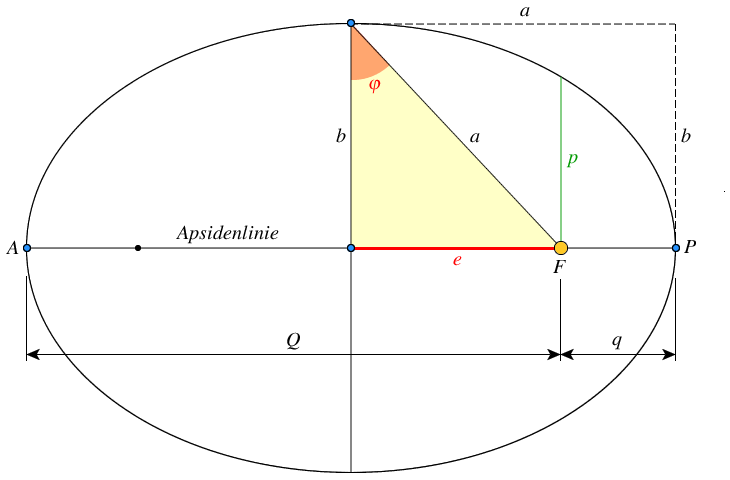
Ellipse
Geometrie
$a$ = große Halbachse
$b$ = kleine Halbachse
$q = a\cdot\left( 1-\epsilon \right)$ = Periheldistanz
$Q = a\cdot\left( 1+\epsilon \right)$ = Apheldistanz
$\varphi$ = Exzentrizitätswinkel
$\epsilon = \frac{e}{a} = \sin(\varphi)$ = numerische Exzentrizität
$e = a\cdot \epsilon$ = lineare Exzentrizität. Es gilt $e^2 = a^2 - b^2$
$P$ = Perihel (sonnennächster Punkt)
$A$ = Aphel (sonnenfernster Punkt)
$F$ = Brennpunkt (Zentralkörper, z.B. Sonne)
$p = \frac{b^2}{a} = a\cdot \left(1-\epsilon^2\right)$ = Bahnparameter der Ellipse
Die numerische Exzentrizität $\epsilon$ gibt die Abweichung von der Kreisbahn ($\epsilon$ = 0) an.
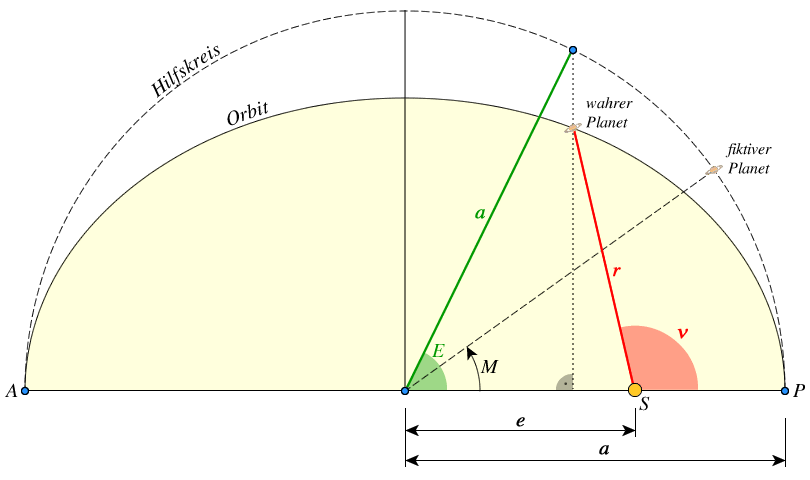
Keplergleichung
$a$ = große Halbachse
$e = a\cdot \epsilon$ = lineare Exzentrizität
$\epsilon = \frac{e}{a}$ = numerische Exzentrizität
$r$ = Radiusvektor, Abstand des Planeten von der Sonne
$\nu$ = wahre Anomalie
$P$ = Perihel (sonnennächster Punkt)
$A$ = Aphel (sonnenfernster Punkt)
$S$ = Brennpunkt (Fokus), hier die Sonne
$E$ = exzentrische Anomalie
$M$ = mittlere Anomalie
Der Hilfskreis hat den Radius der großen Halbachse $a$.
Die Keplergleichung nimmt den Umweg über die exzentrische Anomalie $E$:
$$M = E - \epsilon \cdot \sin(E)\tag{1}$$
Diese Gleichung muss nach $E$ aufgelöst werden. Das erfolgt über die Newtonsche Iteration.
$$E_{i+1} = E_i + \frac{M + \epsilon \cdot \sin(E_i) - E_i}{1 - \epsilon \cdot \cos(E_i)}\tag{2}$$ mit $|E_{i+1} - E_i| = h_{i+1}$. Man startet mit $E_0 = M$ und iteriert etwa 6mal, dann ist die Differenz $h_{i+1} \lt 0.00001$. Die wahre Anomalie $\nu$ wird dann mit der Barkerschen Gleichung berechnet:
$$\tan \left(\frac{\nu}{2}\right) = \sqrt{\frac{1 + \epsilon}{1 - \epsilon}} \cdot \tan\left(\frac{E}{2}\right)\tag{3}$$
Mittelpunktsgleichung
Für kleine Exzentrizitäten $\epsilon$ kann man - anstatt einer iterativen Lösung der Keplergleichung - auf die Mittelpunktsgleichung zurückgreifen. Die Mittelpunktsgleichung wird für gewöhnlich mit $C$ bezeichnet („equation of the center“) und ist eine Reihenentwicklung mit den Variablen $\epsilon$ und $M$. Es gilt
$$C = \nu - M\tag{4}$$
Die Reihenentwicklung lautet
| Tabelle 1 |
|---|
| \[\begin{align} \nu - M = & + \left( {2\epsilon - \frac{1}{4}{\epsilon ^3} + \frac{5}{{96}}{\epsilon ^5} + \frac{{107}}{{4608}}{\epsilon ^7} + \ldots } \right) \cdot \sin (M) \hfill \\ & + \left( {\frac{5}{4}{\epsilon ^2} - \frac{{11}}{{24}}{\epsilon ^4} + \frac{{17}}{{96}}{\epsilon ^6} - \ldots } \right) \cdot \sin (2M) \hfill \\ & + \left( {\frac{{13}}{{12}}{\epsilon ^3} - \frac{{43}}{{64}}{\epsilon ^5} + \frac{{95}}{{512}}{\epsilon ^7} - \ldots } \right) \cdot \sin (3M) \hfill \\ & + \left( {\frac{{103}}{{96}}{\epsilon ^4} - \frac{{451}}{{480}}{\epsilon ^6} + \ldots } \right) \cdot \sin (4M) \hfill \\ & + \left( {\frac{{1097}}{{960}}{\epsilon ^5} - \frac{{5957}}{{4608}}{\epsilon ^7} + \ldots} \right) \cdot \sin (5M) \hfill \\ & + \left( {\frac{{1223}}{{960}}{\epsilon ^6} - \ldots } \right) \cdot \sin (6M) \hfill \\ & + \left( {\frac{{47273}}{{32256}}{\epsilon ^7} - \ldots } \right) \cdot \sin (7M) \hfill \\ \end{align} \] |
Für sehr kleine Exzentrizitäten kann man auch die höheren Potenzen von $\epsilon$, z.B. $\epsilon^4,\,\epsilon^5\ldots$ usw. weglassen. Das Ergebnis erhält man in Radiant, durch Multiplikation mit dem Faktor $\frac{180}{\pi}$ kann es in Grad umgerechnet werden. Die Mittelpunktsgleichung $C$ wird dann zur mittleren Anomalie $M$ addiert und man erhält sofort die wahre Anomalie $\nu$.
Eine Anwendung der Mittelpunktsgleichung ist z.B. bei der schnellen Bestimmung der Sonnenposition zu sehen.
Tabelle: Fehlergröße für die Mittelpunktsgleichung, in Bogensekunden
| Tabelle 2 | ||
|---|---|---|
| Exzentrizität $\epsilon$ | Terme bis $\epsilon^3$ | Terme bis $\epsilon^5$ |
| $0.03$ | $0\overset{''}{.}24$ | $0\overset{''}{.}0003$ |
| $0.05$ | $1\overset{''}{.}80$ | $0\overset{''}{.}007$ |
| $0.10$ | $30''$ | $0\overset{''}{.}45$ |
| $0.15$ | $152''$ | $5''$ |
| $0.20$ | $483''$ | $29''$ |
| $0.25$ | $1183''$ | $111''$ |
| $0.30$ | $2456''$ | $331''$ |
Dem Thema „Lösung der Keplergleichung“ ist ein eigenes Kapitel gewidmet.
Radiusvektor
Der Radiusvektor $r$ wird mit der folgenden Gleichung ermittelt:
$$r = \frac{a \cdot (1 - \epsilon^2)}{1 + \epsilon \cdot \cos(\nu)}\tag{5}$$
Das Argument der Breite $u$ bekommt man mit $u = \omega + \nu$. Während die wahre Anomalie vom Perihel aus gemessen wird, liegt der Bezugspunkt von $u$ beim aufsteigenden Knoten. Den Wert braucht man zum Wechsel in die Ekliptik.
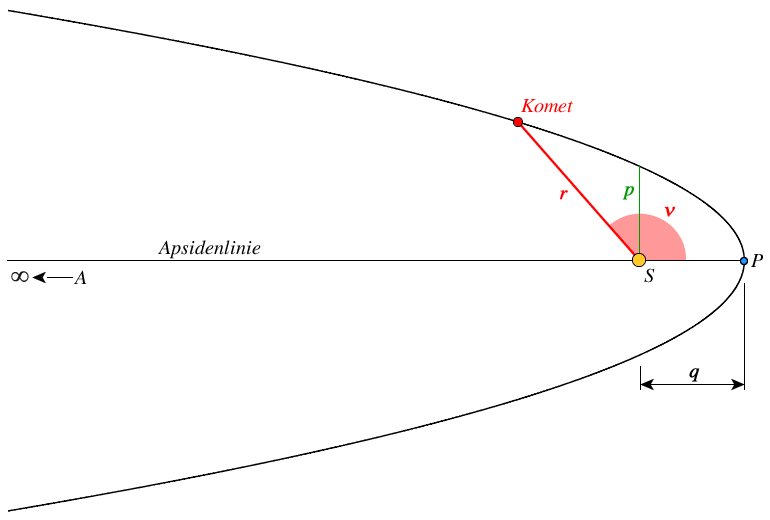
Parabel
Geometrie
$a$ = große Halbachse (a $\rightarrow\infty$)
$P$ = Perihel (sonnennächster Punkt)
$S$ = Brennpunkt (Fokus), hier die Sonne
$r$ = Radiusvektor, Abstand des Kometen von der Sonne
$q$ = Periheldistanz
$\nu$ = wahre Anomalie des Kometen
$p$ = Bahnparameter
$t_0$ = Zeitpunkt des Periheldurchgangs
Eine Parabel hat eine numerische Exzentrizität $\epsilon$ = 1.
Barkersche Gleichung
Die Barkersche Gleichung bestimmt die wahre Anomalie $\nu$ als Funktion der Zeit.
\[\begin{align} \frac{1}{3}\cdot\tan^3\left(\frac{\nu}{2}\right) + \tan\left(\frac{\nu}{2}\right) = \sqrt{\frac{G\cdot (M_S + m)}{2\cdot q^3}}\cdot(t - t_0) \end{align}\tag{6}\]
$G$ und $M_S$ werden in den Wichtige Konstanten erläutert. $m$ ist hier die Masse des Kometen. Diese obige Gleichung muss jetzt aufgelöst werden. Mit den Hilfswerten
$$A = \frac{3}{2}\cdot\sqrt{\frac{G\cdot (M_S + m)}{2\cdot q^3}}\tag{6}$$
\[\begin{align} B = \sqrt[3]{A + \sqrt{A^2 + 1}} \quad \text{und} \quad \frac{1}{B} = \sqrt[3]{\sqrt{A^2 + 1} - A} \end{align}\tag{8}\]
gilt
$$\tan\left(\frac{\nu}{2}\right) = B - \frac{1}{B}\tag{9}$$
und für $A \neq 0$ schreibt man:
\[\begin{align} \tan\left(\frac{\nu}{2}\right) = \pm\frac{2}{\tan\left[2\cdot \arctan\left(\sqrt[3]{\tan\left(\frac{1}{2}\cdot \arctan\left(\frac{1}{|A|}\right)\right)}\right)\right]} \end{align}\tag{10}\]
Radiusvektor
Der Radiusvektor $r$ lautet: $$r = \frac{2\cdot q}{1 + \cos(\nu)}\tag{11}$$
Das Argument der Breite $u$ bekommt man mit $u = \omega + \nu$. Während die wahre Anomalie vom Perihel aus gemessen wird, liegt der Bezugspunkt von $u$ beim aufsteigenden Knoten. Den Wert braucht man zum Wechsel in die Ekliptik.
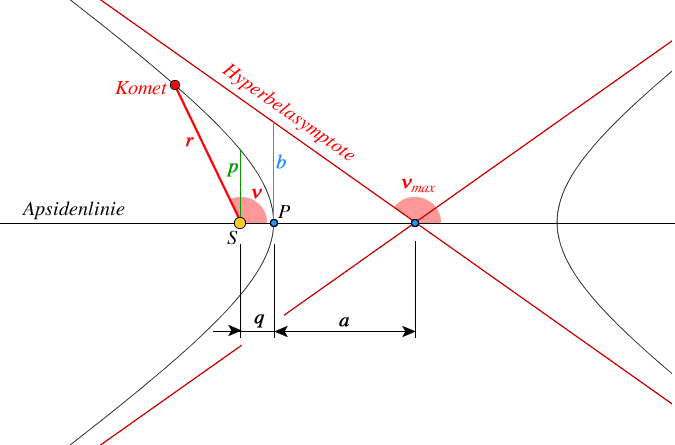
Hyperbel
Geometrie
$a$ = große Halbachse ($a < 0$)
$b$ = kleine Halbachse
$P$ = Perihel (sonnennächster Punkt)
$S$ = Brennpunkt (Fokus), hier die Sonne
$\epsilon = \frac{e}{a}$ = numerische Exzentrizität ($\epsilon > 1$)
$r$ = Radiusvektor, Abstand des Kometen von der Sonne
$q$ = Periheldistanz
$\nu$ = wahre Anomalie des Kometen
$p$ = Bahnparameter
Zu beachten ist hier, dass die große Halbachse $a$ einer Hyperbelbahn definitionsgemäß eine negative Größe ist!
Keplergleichung
Bei der Hyperbelbahn wird die exzentrische Anomalie mit $H$ bezeichnet. Die Berechnung von $H$ und des Radiusvektors $r$ erfolgt analog zur Ellipse. Startwert ist wieder die mittlere Anomalie $M_h$:
$$H_{i+1} = H_i - \frac{\epsilon\cdot \sinh(H_i) - H_i - M_h}{\epsilon\cdot \cosh(H_i) - 1}\tag{12}$$
Die Iteration ist solange zu wiederholen, bis $|H_{i+1} − H_i| \lt 10^{−8}$ gilt. Hat man die exzentrische Anomalie $H$ gefunden, so ist die korrespondierende wahre Anomalie $\nu$:
$$\tan\left(\frac{\nu}{2}\right) = \sqrt{\frac{\epsilon + 1}{\epsilon - 1}}\cdot \tanh\left(\frac{H}{2}\right)\tag{13}$$
Radiusvektor
Der Radius lautet:
$$r = a\cdot \frac{1 - \epsilon^2}{1 + \epsilon\cdot \cos(\nu)}\tag{14}$$
Das Argument der Breite $u$ bekommt man mit $u = \omega + \nu$. Während die wahre Anomalie $M_h$ vom Perihel aus gemessen wird, liegt der Bezugspunkt von $u$ beim aufsteigenden Knoten. Den Wert braucht man zum Wechsel in die Ekliptik.