Eine “quadratische Funktion” hat die allgemeine Form

\(f(x) = a x^2 + b x + c\)

Im ersten Term kommt das \(x\) quadratisch vor, im zweiten Term nur als \(x\), und im dritten Term kommt das \(x\) gar nicht vor. Die Werte \(a, b, c\)  heißen Koeffizienten. Die Koeffizienten können natürlich positiv oder negativ sein.

Man nennt

• den ersten Term \(a x^2\)  den quadratischen Term
• den zweiten Term \(b x\)  den linearen Term
• den letzten Term \(c\)  den konstanten Term.

Je nachdem, welche Werte nun die Koeffizienten annehmen, sieht die Funktion aus.

Nachstehend kann man ein Geogebra-Applet aufrufen, bei dem man die Werte für \(a, b, c\) einstellen kann, um dann zu beobachten, wie sich die Funktion verändert. (Man muss Java-Applets im Browser zulassen)

→ Applet zu quadratischen Funktionen anzeigen

Im Speziellen beobachtet man:

• Wenn \(a\) positiv ist, ist die Parabel nach oben offen.
• Wenn \(a\) negativ ist, ist die Parabel nach unten offen.
• Der Wert \(c\) gibt an, wo die Funktion die y-Achse schneidet. Das ist leicht einzusehen, denn wenn man für \(x=0\)  einsetzt, bleibt ja nur der konstante Term \(c\)  übrig. Verändert man also nur den Wert \(c\), wird die Funktion nur in y-Richtung verschoben, ohne dass sich die “Form” der Funktion verändert.
• Ist \(c=0\), dann geht die Funktion durch den Ursprung \((0|0)\)
• Der Wert \(b\) verschiebt die Funktion in beide Richtungen.
• Wenn der \(a = 0\) ist, fällt der quadratische Term weg und man erhält eine lineare Funktion, ein Gerade!
• Ist der Koeffizient \(a>1\), wird die Funktion noch oben hin “gestreckt”, ist \(a<-1\), erfolgt die Streckung nach unten (im Vergleich mit der Normalparabel, siehe unten).
• Ist \(-1 < a <1\), liegt also zwischen -1 und 1, wird die Funktion “gestaucht” (im Vergleich mit der Normalparabel, siehe unten).

Weiters ist der Scheitel der Funktion als roter Punkt eingezeichnet. Die Funktion hat dort ein Minimum oder ein Maximum, und zwar

• wenn der Koeffizient \(a\) positiv ist (die Parabel also nach oben offen ist), ist der Scheitel ein Minimum der Funktion.
• wenn der Koeffizient \(a\) negativ ist (die Parabel also nach unten offen ist), ist der Scheitel ein Maximum der Funktion.

Die strichlierte Kurve ist die ⇒ Ortskurve (ebenfalls eine Parabel), auf der sich der Scheitelpunkt bewegt, wenn man nur den Faktor \(b\) der quadratischen Funktion verändert.

Die allgemeine quadratische Gleichung kann mit der ⇒ “Mitternachtsformel” gelöst werden.

Die Normalparabel

Als Normalform der quadratischen Gleichung wir jene Gleichung bezeichnet, bei der der Koeffizient des quadratischen Terms \(a=1\) ist. Man schreibt dann

\(x^2+px+q=0\)

Es kommen bei der Normalform nur mehr zwei Koeffizienten, \(p\) und \(q\), vor. Die Normalform der quadratischen Gleichung kann mit der ⇒ “p-q-Formel” gelöst werden.

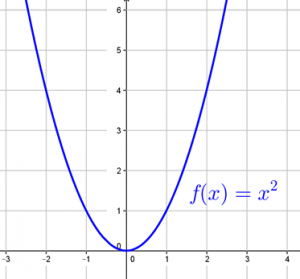
Als Normalparabel bezeichnet man die Funktion dann, wenn die Koeffizienten \(a=1\),  \(b=0\)  und \(c=0\) sind. Man erhält also die Funktion

\(f(x) = a x^2 + \underbrace {b\,x}_{ = 0} + \underbrace {c}_{ = 0}\)

Hier kommt nur mehr der quadratische Term vor, und der Koeffizient \(a=1\). Man könnte also auch schreiben

\(f(x)=1\cdot x^2\).

Da \(a>0\) ist, ist die Normalparabel oben offen.