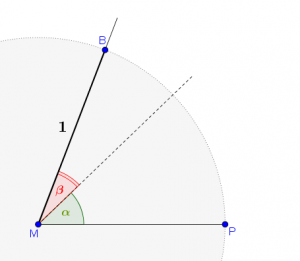Konstruiere um einen Punkt \(M\) einen Kreis mit dem Radius \(r=1\) (Einheitskreis).

Zeichne den waagrechten Schenkel \(\overline{MP}\) ein.

Zeichne ausgehend vom Schenkel \(\displaystyle \overline{{MP}}\) einen beliebigen Winkel \(\alpha\) und daran anschließend einen beliebigen Winkel \(\beta\) ein.

Punkt \(B\) ergibt sich als Schnittpunkt von Einheitskreis und dem Schenkel von \(\beta\).

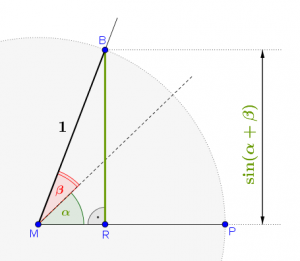Konstruiere die Normale durch \(B\) auf den Schenkel \(\displaystyle \overline{{MP}}\) und bezeichne den Fußpunkt mit \(R\).

Im Dreieck \(\displaystyle \triangle MBR\) ist nun die Strecke \(\displaystyle \overline{{BR}}\) die Gegenkathete zum gesamten Winkel \((\alpha + \beta)\), es gilt also

\(\displaystyle \sin (\alpha +\beta )=\frac{{GK}}{{HYP}}=\frac{{\overline{{BR}}}}{1}=\overline{{BR}}\)

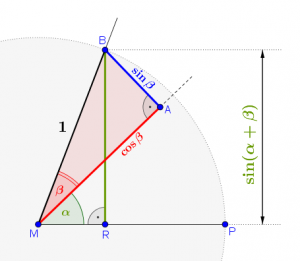Zeichne einen Punkt \(A\) auf dem gemeinsamen Schenkel von \(\alpha\) und \(\beta\) so ein, dass \(\displaystyle \overline{AB}\) normal auf \(\displaystyle \overline{MA}\) steht.

Es entsteht das rote rechtwinkelige Dreieck \(\displaystyle \triangle MAB\). In diesem Dreieck ist die Hypotenuse \(r=1\) und gemäß der Definition von Sinus und Cosinus gilt:

\(\displaystyle \sin \beta =\frac{{GK}}{{HYP}}=\frac{{\overline{{AB}}}}{1}\Rightarrow \overline{{AB}}=\sin \beta \)

\(\displaystyle \cos \beta =\frac{{AK}}{{HYP}}=\frac{{\overline{{MA}}}}{1}\Rightarrow \overline{{MA}}=\cos \beta \)

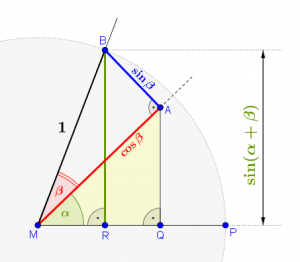Konstruiere die Normale durch den Punkt \(A\) auf den Schenkel \(\displaystyle \overline{{MP}}\) und bezeichne den Fußpunkt mit \(Q\).

Das gelbe rechtwinkelige Dreieck \(\triangle MAQ\) besitzt als Hypotenuse die Strecke \(\overline{MA} = \cos \beta\) (Siehe Schritt 3).

Die Strecke \(\overline{AQ}\) ist die Gegenkathete zum Winkel \(\alpha\), daher gilt

\(\displaystyle \sin \alpha =\frac{{GK}}{{HYP}}=\frac{{\overline{{QA}}}}{{\overline{{MA}}}}=\frac{{\overline{{QA}}}}{{\cos \beta }}\).

Daher folgt

\(\displaystyle \overline{{QA}}=\sin \alpha \cdot \cos \beta \)

 

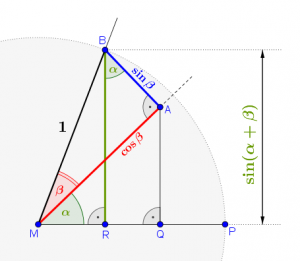Der Winkel \(\alpha\) wird von den Schenkeln \(\displaystyle \overline{MP}\) und \(\displaystyle \overline{MA}\) eingeschlossen. Man sieht in der Skizze

• \(\displaystyle \overline{BR}\) steht normal auf \(\displaystyle \overline{MP}\)
• \(\displaystyle \overline{AB}\) steht normal auf \(\displaystyle \overline{MA}\)

Daher entspricht der Winkel \(\angle RBA\) beim Punkt \(B\) ebenfalls dem Winkel \(\alpha\)! (Normalwinkel)

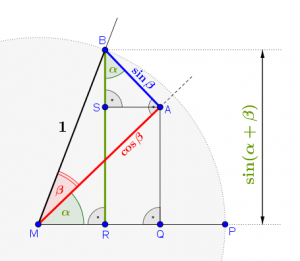Konstruiere die Normale auf die Strecke \(\overline{BR}\) durch den Punkt \(A\). Den Fußpunkt bezeichne mit \(S\).

Das rechtwinkelige Dreieck \(\triangle ASB\) hat als Hypotenuse die Strecke \(\overline{AB} = \sin \beta\) (Siehe Schritt 3).

Es gilt daher

\(\displaystyle \cos \alpha =\frac{{AK}}{{HYP}}=\frac{{\overline{{BS}}}}{{\overline{{BA}}}}=\frac{{\overline{{BS}}}}{{\sin \beta }}\) und daher

\(\displaystyle \overline{{BS}}=\cos \alpha \cdot \sin \beta \)

Die gesamte Strecke \(\overline{BR}\) entspricht laut Schritt 2 dem \(\sin (\alpha + \beta)\)

Es gilt daher

\(\displaystyle \overline{{BR}}=\overline{{RS}}+\overline{{BS}}=\overline{{QA}}+\overline{{BS}}\)

Setzt man die Strecke \(\overline{QA}\) aus Schritt 4 und Strecke \(\overline{BS}\) aus Schritt 6 ein, ergibt sich

\(\displaystyle \underbrace{{\sin (\alpha +\beta )}}_{{\overline{{BR}}}}=\underbrace{{\sin \alpha \cdot \cos \beta }}_{{\overline{{QA}}}}+\underbrace{{\cos \alpha \cdot \sin \beta }}_{{\overline{{BS}}}}\)

q.e.d.