Dies ist eine alte Version des Dokuments!
Inhaltsverzeichnis
Koordinatentransformation
Bahnebene
Der Bezug ist der Schnittpunkt Ekliptik/Bahnebene. Vorher war es mit der wahren Anomalie $\nu$ das Perihel. Man bewegt sich in der Bahnebene des Himmelsobjekts. Es gilt:
$$\begin{align} x &= r \cdot \cos(u) \\ y &= r \cdot \sin(u) \\ z &= 0\end{align}$$
$u$ ist das Argument der Breite mit $u = \nu + \omega $. aus dem Abschnitt über die Kegelschnitte.
$i$ = Inklination, Bahnneigung der Bahnebene zur Ekliptik
$\Omega$ = Knotenlänge, Länge des Schnittpunkts Bahnebene/Ekliptik vom Frühlingspunkt 
gemessen. Der Winkel liegt in der Ekliptik.
$\omega$ = Länge vom aufsteigenden Knoten zum Perihel, dieser Winkel liegt in der Bahnebene.
$\varpi = \Omega + \omega$ = Perihellänge, gemessen vom Frühlingspunkt zum Perihel. Der Winkel liegt in zwei verschiedenen Ebenen und ist deshalb ein unechter oder gebrochener Winkel.
Zu den genannten Winkeln siehe Bahnelemente.
Heliozentrische Koordinaten
Die Bahnebene wird über die Inklination $i$ in die Ekliptik gekippt und dann um die Knotenlänge $\Omega$ zum Frühlingspunkt gedreht. Das ist der neue Bezugspunkt im System.
| \[\begin{align} \cos (l)\cdot\cos (b) &=\, x = \cos (u)\cdot\cos (\Omega) - \sin (u)\cdot\cos (i)\cdot\sin (\Omega) \\ \sin (l)\cdot\cos (b) &=\, y = \cos (u)\cdot\sin (\Omega) + \sin (u)\cdot\cos (i)\cdot\cos (\Omega) \\ \sin (b) &=\, z = \sin (u)\cdot\sin (i) \end{align}\] |
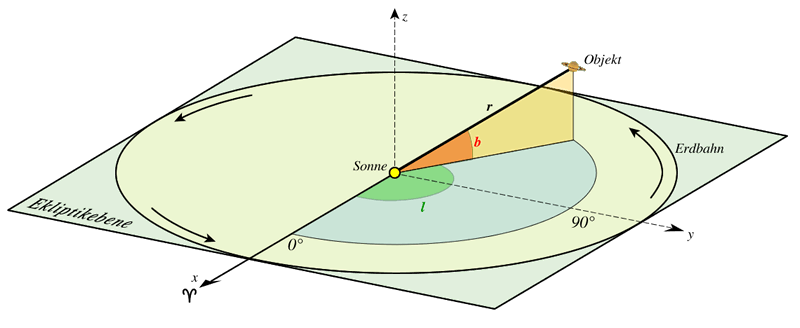
Die Auflösung der karthesischen Koordinaten erfolgt im Abschnitt über sphärische Koordinaten. Man erhält die heliozentrisch ekliptikalen Koordinaten $l$ (Länge) und $b$ (Breite).
Geozentrische Koordinaten
ekliptikal
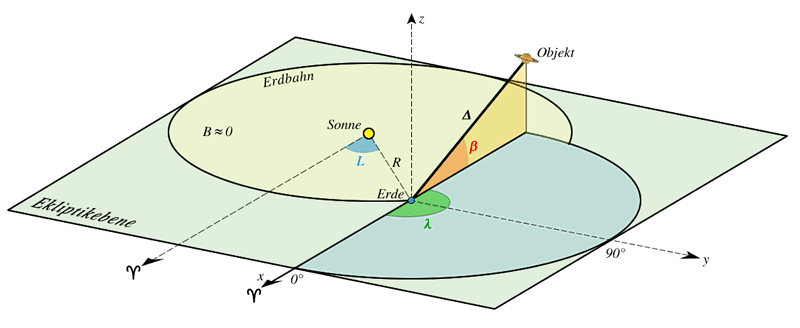
An dieser Stelle wird die Sichtlinie von der Sonne aus zur Erde verschoben. Man bleibt in der Ekliptik. $L$, $B$ und $R$ sind die heliozentrisch ekliptikalen Koordinaten der Erde. Der Frühlingspunkt bleibt Bezugspunkt.
| \[\begin{align} \Delta\cdot\cos(\lambda)\cdot\cos(\beta) &=\, x = r\cdot\cos(l)\cdot\cos(b) - R\cdot\cos(L)\cdot\cos(B) \\ \Delta\cdot\sin(\lambda)\cdot\cos(\beta) &=\, y = r\cdot\sin(l)\cdot\cos(b) - R\cdot\sin(L)\cdot\cos(B) \\ \Delta\cdot\sin(\beta) &=\, z = r\cdot\sin(b) - R\cdot\sin(B) \end{align}\] |
Die Auflösung der karthesischen Koordinaten erfolgt im Abschnitt über sphärische Koordinaten. Man erhält die geozentrisch ekliptikalen Koordinaten $\lambda$ (Länge), $\beta$ (Breite) und die geozentrische Distanz $\Delta$ des Himmelsobjekts zur Erde.
äquatorial
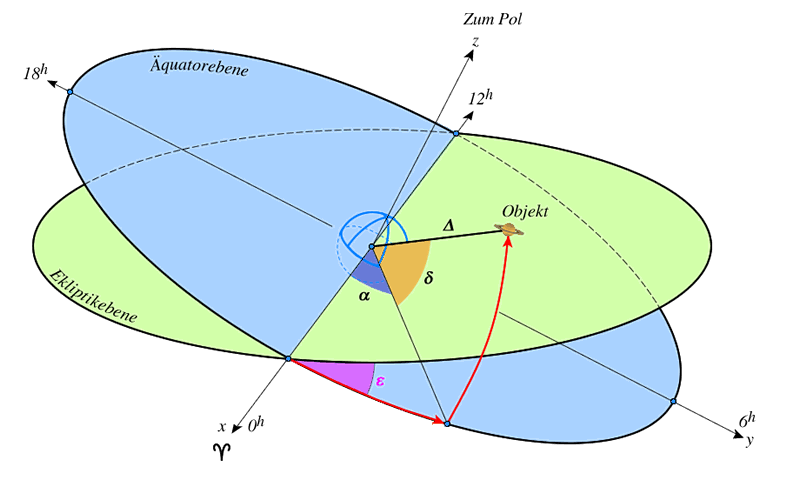
Mit dem äquatorialen Koordinaten wechselt man in ein rotierendes System. Dazu muss die Ekliptikschiefe $\varepsilon$ eingeführt werden, denn um die wird die Eklipitikebene in das äquatoriale System gekippt. Der Frühlingspunkt bleibt Bezugspunkt.
Für die Epoche J2000 gilt: $\varepsilon = 23^\circ 26'21\overset{''}{.}448 = 23\overset{\circ}{.}43929111$
| \[\begin{align} \cos (\delta)\cdot \cos (\alpha) &=\, x = \cos (\beta)\cdot \cos (\lambda) \\ \cos(\delta)\cdot \sin(\alpha) &=\, y = \cos(\beta)\cdot \sin(\lambda)\cdot \cos(\varepsilon) - \sin (\beta)\cdot \sin (\varepsilon) \\ \sin (\delta) &=\, z = \cos (\beta)\cdot \sin (\lambda)\cdot \sin (\varepsilon) + \sin (\beta)\cdot \cos (\varepsilon) \end{align}\] |
Die Auflösung der karthesischen Koordinaten erfolgt im Abschnitt über sphärische Koordinaten. Man erhält die geozentrisch äquatorialen Koordinaten $\alpha$ (Länge, Rektaszension) und $\delta$ (Breite, Deklination) des Himmelsobjekts zur Erde.
Die Rektaszension wird in Stunden angegeben. $\alpha$ muss anschließend für die Ausgabe durch 24$^h$ geteilt werden. Für die Berechnung verbleibt $\alpha$ in Grad.
topozentrisch
Hier wird wieder die Sichtlinie von dem Erdmittelpunkt an die Erdoberfläche verschoben. Der geozentrische Abstand $\rho$ berücksichtigt die Abplattung des Erdkörpers.
| \[\begin{align} r'\cdot\cos(\alpha')\cdot\cos(\delta') &= x = r\cdot\cos(\alpha)\cdot\cos(\delta) - \rho\cdot\cos(\theta)\cdot\cos(\beta_0) \\ r'\cdot\sin(\alpha')\cdot\cos(\delta') &= y = r\cdot\sin(\alpha)\cdot\cos(\delta) - \rho\cdot\sin(\theta)\cdot\cos(\beta_0) \\ r'\cdot\sin(\delta') &= z = r\cdot\sin(\delta) - \rho\cdot\sin(\beta_0) \end{align}\] |
Die Auflösung der karthesischen Koordinaten erfolgt im Abschnitt über sphärische Koordinaten. Man erhält die topozentrisch äquatorialen Koordinaten $\alpha'$ (Länge), $\delta'$ (Breite) und die topozentrische Distanz $r'$ des Himmelsobjekts zum Beobachter.
Horizontale/Azimutale Koordinaten
In diesem Abschnitt wechselt man endgültig ist das bürgerliche System, das man als Beobachter kennt.
| \[ \begin{align} \cos (h)\cdot \cos (A) &= x = \cos (\delta')\cdot \cos(\theta - \alpha')\cdot \sin (\beta_0) - \sin (\delta')\cdot \cos(\beta_0) \\ \cos (h)\cdot \sin (A) &= y = \cos (\delta')\cdot \sin (\theta - \alpha') \\ \sin (h) &= z = \cos (\delta')\cdot \cos (\theta - \alpha')\cdot \sin (\beta_0) + \sin (\delta')\cdot \sin (\beta_0) \end{align} \] |
Die Auflösung der karthesischen Koordinaten erfolgt im Abschnitt über sphärische Koordinaten. Man erhält die azimutalen oder horizontalen Koordinaten $A$ (Azimut) und $h$ (Höhe).
Baryzentrum
Das Baryzentrum ist nichts anderes als der Schwerpunkt eines Systems. Dieser fällt in der Regel nicht mit dem Massenmittelpunkt zusammen. Dies ist für das Erde - Mond System, das Pluto - Charon System und dem Sonnensystem selbst wichtig. Tatsächlich rotiert man um den Schwerpunkt, nicht um den Mittelpunkt.
| \[ \begin{align} r_B \cdot \cos(b_B) \cdot \cos(l_B) &= x = r \cdot \cos(b) \cdot \cos(l) - G \cdot \cos(B) \cdot \cos(L) \\ r_B \cdot \cos(b_B) \cdot \sin(l_B) &= y = r \cdot \cos(b) \cdot \sin(l) - G \cdot \cos(B) \cdot \sin(L) \\ r_B \cdot \sin(b_B) &= z = r \cdot \sin(b) - G \cdot \sin(B) \end{align} \] |
Legende
$l,b,r$ = heliozentrisch - ekliptikale Koordinaten des Planeten
$l_B,b_B,r_B$ = baryzentrisch - ekliptikale Koordinaten des Planeten
$L,B,R$ = heliozentrisch - ekliptikale Koordinaten des Baryzentrums oder der Sonne
$\tau$ = Stundenwinkel des Objekts = Winkel seit dem Meridiandurchgang
$\theta$ = lokale Sternzeit des Beobachter in Grad, siehe Abschnitt Sternzeit. Es gilt: $\tau = \theta - \alpha'$
$\alpha,\delta$ = geozentrische äquatoriale Koordinaten des Himmelsobjekts
$\alpha',\delta',r'$ = topozentrische äquatoriale Koordinaten des Himmelsobjekts
$\lambda_0,\beta_0$ = geographische Länge und Breite
$R_E$ = Erdradius, siehe das Kapitel über die Wichtige Konstanten.
$\rho$ = geozentrischer Abstand des Beobachters ($\neq R_E$)
$\Delta$ = geozentrischer Abstand des Planeten
$M$ = Erdmittelpunkt