Hat man die Koordinaten $\vec{r}$ und $\dot{\vec{r}} = \vec{v}$, so kann man die kinetische Energie $T$ und die potentielle Energie $V \lt 0$ mit der folgenden Beziehung berechnen:

$$E = T + V = \frac{1}{2}\cdot m\cdot v^2 + V(r)\tag{1} \qquad\text{mit}\qquad \vec{v}\cdot\vec{v} = v^2$$

mit $E$ als der Gesamtenergie. Sie wird noch als Erhaltungsgrösse der Zeit $t$ behandelt. Die Ableitung nach der Zeit $t$ und Teilung durch den Impuls $\vec{p} = m\cdot\vec{v}$ ergibt eine Differentialgleichung 2. Ordnung:

$$0 = \ddot{r} + \frac{1}{m}\cdot\frac{d}{dr}V(r)\tag{2}$$

Daraus ergeben sich die Newtonschen Kraftgleichungen:

$$F = m\cdot \ddot{r} \qquad und\qquad K = - \frac{d}{dr}V(r) \qquad mit\qquad 0 = F + K\tag{3}$$

Es ist auch umgekehrt die Integration der Energiegleichung (1) möglich:

$$p = \sqrt{2\cdot m}\cdot \int \sqrt{E - V(r)} \text{d}r\tag{4}$$

und

$$t = \sqrt{\frac{m}{2}}\cdot \int \frac{1}{\sqrt{E - V(r)}} \text{d}r\tag{5}$$

Die Koordinaten $\vec{r}$ und $\vec{v}$ sind:

$$\vec{r} = r \left(\begin{split} & \cos(\nu) \\ & \sin(\nu) \end{split}\right)\tag{6}$$

$$\vec{v} = \dot{\vec{r}} = \dot{r} \left(\begin{split} & \cos(\nu) \\ & \sin(\nu) \end{split}\right) + r\cdot\dot{\nu} \left(\begin{split} - & \sin(\nu) \\ + & \cos(\nu) \end{split}\right)\tag{7}$$

Daraus folgt für $v^2$:

$$v^2 = \dot{r}^2 + r^2\cdot\dot{\nu}^2\tag{8}$$

Die modifizierte Energiegleichung lautet dann:

$$E = \frac{1}{2}\cdot m\cdot\dot{r}^2 + \frac{1}{2}\cdot m\cdot r^2\dot{\nu}^2 + V(r)\tag{9}$$

1. Keplergesetz: Alle Planeten bewegen sich auf elliptischen Bahnen, in deren einem der beiden Brennpunkte sich die Sonne befindet.

$$r = \frac{p}{1 + \epsilon\cdot\cos(\nu)}\tag{6}$$

2. Keplergesetz: Ein von der Sonne zum Planeten gezogener Fahrstrahl (Radius) überstreicht in gleichen Zeiten gleichgrosse Flächenabschnitte $\vec{F}$.

$$\vec{F} = \frac{\vec{L}_{\nu}}{2\cdot m} T\tag{7} \qquad\text{mit}\qquad T = t_1 - t_2$$

Abb. 1: Das 2. Keplergesetz. Die hellblauen Flächen sind die Flächenabschnitte $\vec{F}$.

$\nu$ = wahre Anomalie

3. Keplergesetz: Das Quadrat der Umlaufzeit $U$ eines Planeten verhält sich wie der Kubus (dritte Potenz) seines mittleren Bahnabstands.

$$\frac{U^2}{r^3} = \frac{4\cdot\pi^2}{G\cdot M_S}\tag{8}$$

Formt man das 3. Keplergesetz für $r = a = 1 \text{AE}$ um zu

$$U_s = \frac{2\pi}{k}\tag{9}$$

so erhält man die siderische Umlaufszeit $U_s$ der Erde. Die gaußsche Gravitationskonstante $k = \sqrt{GM_S}$ ist als eine fundamentale Naturkonstante für die Stärke der Gravitation verantwortlich.

Sie ist definiert mit

$$k = \frac{2\pi}{U_s}\tag{10}$$

und $U_s$ als das siderische Jahr.

$$\deg(k) = n = \frac{360^{\circ}}{U_s}\tag{11}$$

liefert die mittlere tägliche Bewegung n der Erde um die Sonne.

Die Herleitung: Beruhend auf der Energiebilanzgleichung E mit dem Gravitationpotential $$V(r) = - G \frac{m M_S}{r}\tag{12}$$

$$E = \frac{1}{2} \cdot m\cdot \dot{r}^2 + \frac{1}{2}\cdot m\cdot r^2 \dot{\nu}^2 - G \frac{m\cdot M_S}{r}\tag{13}$$

resultiert aus der Ableitung nach r die Zentripetalkraft $\vec{F}_z$ (links) bzw. die Gravitationskraft $\vec{F}_g$ (rechts): $$F_z = m\cdot\dot{\nu}^2\cdot r = - F_g = G\cdot\frac{M m}{r^2} \Leftrightarrow \frac{U^2}{r^3} = \frac{4\pi^2}{G M} = \text{konst.} \qquad\text{mit}\qquad\dot{\nu} = \omega = \frac{2\pi}{U}\tag{14}$$

Das Verhältnis der Umlaufszeit U zur Bahngrösse r ist zeitlich konstant und damit eine Erhaltungsgrösse. In einem Relativsystem mit r = r$_1$ – r$_2$ gilt, wobei man in vielen Anwendungen die kleinere Masse nicht vernachlässigen kann: $$\frac{U^2}{r^3} = \frac{4\pi^2}{G \left(m_1 + m_2\right)}\tag{15}$$

Der Runge - Lenz Vektor $\vec{R}_L$ (Abb.2) ist wie E und L$_{\nu}$ eine Erhaltungsgrösse.

$$\vec{A} = (m\cdot\dot{\vec{r}} \times \vec{L}_{\nu}) - G\cdot M_S\cdot m^2 \frac{\vec{r}}{r} = \text{konst.}\tag{16}$$

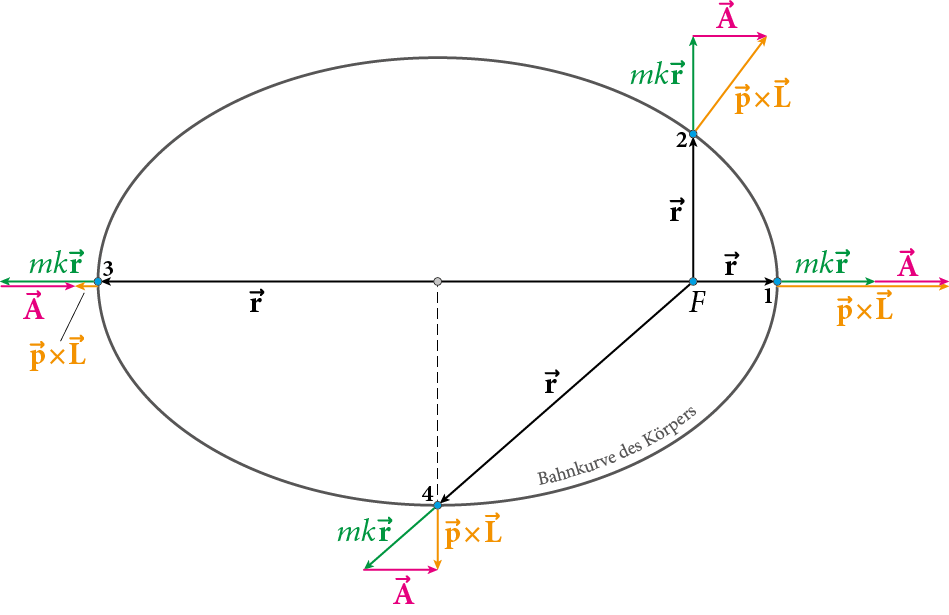Abb. 2: Der Laplace-Runge-Lenz-Vektor A

Der Runge - Lenz Vektor wird auch als Perizentrumsvektor bezeichnet, weil er die in Richtung des Perihels der Planetenbahn zeigt. Nach skalarer Multiplikation mit $\vec{r}$ unter Berücksichtigung der nachfolgenden Relationen

$$\vec{r}\cdot\vec{A} = r\cdot A\cos(\nu), \quad \vec{r}\cdot\vec{r} = |\vec{r}|^2 = r^2\tag{17}$$

und

$$\vec{r}\cdot (m\cdot\dot{\vec{r}}\times\vec{L}_{\nu}) = - (m\cdot\dot{\vec{r}}\times\vec{r})\cdot \vec{L}_{\nu} = |\vec{L}_{\nu}|^2\tag{18}$$

erhält nach einigen Umformungen die folgende Relation

$$r \left(\frac{A}{G\cdot M_S\cdot m^2}\cos(\nu) + 1\right) = \frac{L_{\nu}^2}{G\cdot M_S\cdot m^2}\tag{19}$$

und das resultiert wiederum in die Kegelschnittsgleichung mit

$$\epsilon = \frac{|\vec{A}|}{G\cdot M_S\cdot m^2}\Rightarrow\epsilon\sim A\tag{20}$$