Ein Komet innerhalb der Erdbahn

Ein Komet bewege sich auf einer parabolischen Bahn ($\epsilon = 1$) im Gravitationsfeld der ruhenden Sonne. Seine Bahnebene falle mit der als kreisförmig idealisierten Bahnebene der Erde zusammen. Wie lange bewegt sich der Komet innerhalb der Erdbahn? Eine Störung der Kometenbahn durch die anderen Planeten soll vernachlässigt werden.

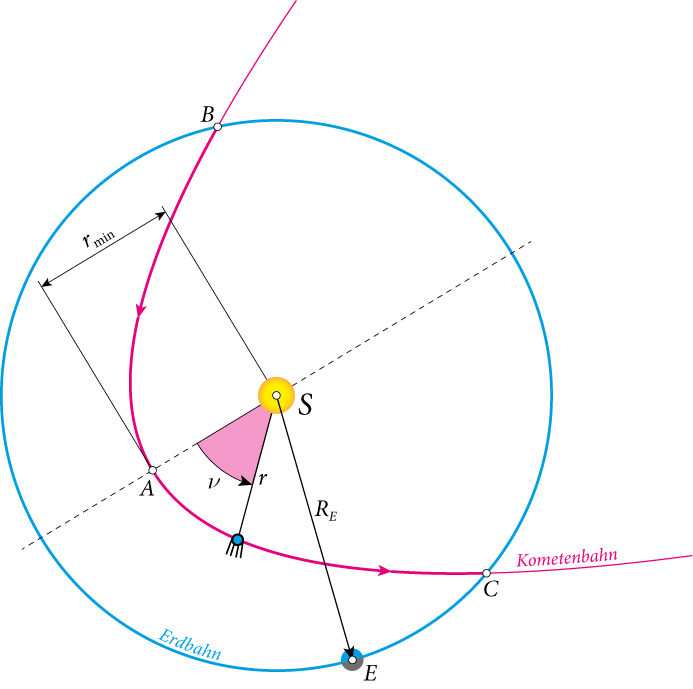Abb. 1: Verlauf einer Kometenbahn

Zuerst wird die Schwerpunktsmasse $\mu$ eingeführt mit

$$\mu = \frac{m\cdot M}{m + M_{\odot}}\tag{1}$$

Die entsprechende Energiegleichung lautet

$$E = \frac{1}{2}\cdot\mu\cdot\dot{r}^2 + \frac{L_{\nu}^2}{2\cdot\mu\cdot r^2} - G\cdot \frac{m\cdot M_{\odot}}{r}\tag{2}$$

zusammen mit der korrespondierenden Differentialgleichung (DGL):

$$0 = \mu\cdot\ddot{r} - \frac{L_{\nu}^2}{\mu\cdot r^3} + G\cdot \frac{m\cdot M_{\odot}}{r^2}\tag{3}$$

Die Lösung der DGL ist die bekannte Kegelschnittsgleichung

$$r(\nu) = \frac{p}{1 + \epsilon\cdot \cos(\nu)}\tag{4}$$

mit

$$\epsilon = \sqrt{1 + \frac{2\cdot L_{\nu}^2}{G^2}\cdot \frac{m^2\cdot M^2}{\mu}\cdot E}\tag{5}$$

und

$$p = \frac{L_{\nu}^2}{G\cdot M_{\odot}\cdot m^2}\tag{6}$$

Befindet sich der Komet im Perihel ist seine radiale Geschwindigkeit $\dot{r}$ gleich Null. $r$ erreicht gleichzeitig sein Minimum. Es gilt die Bedingung:

$$\dot{r}_{min} = 0$$

Daraus folgt via Energiegleichung (2):

$$r_{min} = \frac{L_{nu}^2}{2\cdot\mu}\cdot \frac{1}{G\cdot m\cdot M_{\odot}}\tag{7}$$

Nun muss die Verweildauer des Kometen bestimmt werden. Dazu formt man die Energiegleichung (2) zum Zeitintegral um:

$$t = \sqrt{\frac{\mu}{2\cdot G\cdot m\cdot M_{\odot}}}\cdot \int\limits^{R_E}_{r_{min}} \frac{r}{\sqrt{r - r_{min}}} \mathrm{d}r\tag{8}$$

und integriert zu:

$$t = \frac{2}{3}\cdot\sqrt{\frac{\mu}{2\cdot G\cdot m\cdot M_{\odot}}}\cdot \sqrt{R_E - r_{min}}\cdot (R_E + 2\cdot r_{min})\tag{9}$$

Der Zeitraum $t$ ist nur die Zeit vom Schnittpunkt mit der Erdbahn ($R_E = 1\;AE$) bis zum Perihel des Kometen. Aufgrund der angenommenen Symmetrie der Parabel gilt die Bedingung $T = 2\cdot t$

Setzt man $\frac{dT}{dr_{min}} = 0$ so ist die Lösung für $r_{min}$:

$$r_{min} = \frac{R_E}{2}\tag{10}$$

Der Perihel des Kometen hat den halben Erdabstand (Erinnerung: Erdbahn sei kreisförmig). Damit braucht man $r_{min}$ nur noch in Gleichung (9) einzusetzen und man erhält die Lösung mit $G$, $R_E$ und $M_{\odot}$:

$$T = \frac{4}{3}\cdot\sqrt{\frac{R_E^3}{G\cdot M_{\odot}}} = 6.6958\cdot 10^6\;s \approx 77\overset{d}{.}4977 = 77^d11^h47^m$$