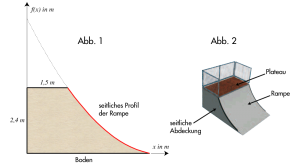
Dies ist ein Beispiel aus der Zentralmatura 2016
Ein Unternehmen, das Skate-Parks errichtet, plant eine neue Minirampe.
Das seitliche Profil der Rampe kann durch eine Parabel 2. Ordnung modelliert werden:
\(f(x)=0,2\cdot {{x}^{2}}-2\cdot x+4,95\quad \quad mit\quad 1,5<x<4,5\)
\(x…\) waagrechte Entfernung von der Rückwand in Metern (m)
\(f(x)…\) Höhe der Rampe in Metern (m) an der Stelle \(x\)
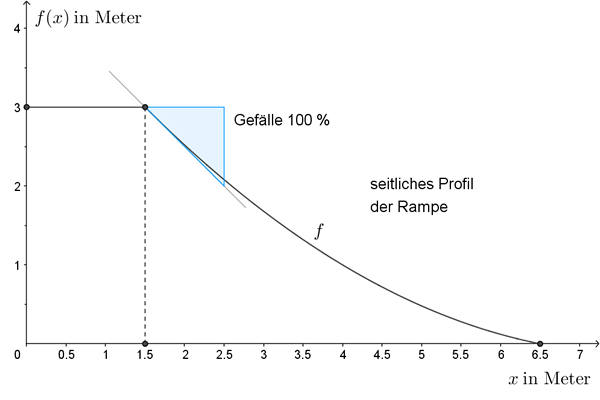
- Berechnen Sie den Inhalt der Querschnittsfläche einer seitlichen Abdeckung.
Entnehmen Sie die dazu notwendigen Werte der Abbildung 1. - Zeigen Sie, dass die gegebene Parabel 2. Ordnung beim Übergang zum Boden keine waagrechte Tangente aufweist.
- Dokumentieren Sie die Berechnung des Winkels zwischen Plateau und Rampe.
4. Auf Kundenwunsch wird eine höhere Rampe errichtet, deren seitliches Profil wieder
durch eine quadratische Funktion \(f\) mit \(f(x)=a\cdot {{x}^{2}}+b\cdot x+c\) beschrieben werden
kann.
Höhe der Rampe: 3 m
Tiefe des Plateaus: 1,5 m
maximales Gefälle: 100 %
Bodenlänge der Rampe: 6,5 m
– Stellen Sie mit den gegebenen Angaben ein Gleichungssystem zur Berechnung der
Koeffizienten dieser quadratischen Funktion auf.
Hinweis zur Aufgabe:
Lösungen müssen der Problemstellung entsprechen und klar erkennbar sein. Ergebnisse sind
mit passenden Maßeinheiten anzugeben.