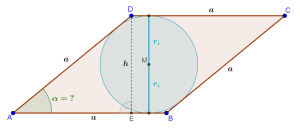
Von einer Raute \(ABCD\) mit der Seitenlänge \(a\) ist bekannt, dass ihr Inkreis die halbe Fläche der Raute hat.
Gesucht: Berechne den Winkel \(\alpha\) beim Punkt \(A\) der Raute, damit diese Bedingung erfüllt ist!
Benögtigte Kenntnisse:
- Zusammenhänge bei der geometrischen Figur Raute
- Gleichungen umformen
- Sinus und Cosinus im rechtwinkeligen Dreieck
- Doppelte und halbe Winkel als Argument der Sinus-Funktion:
\(\sin (2x) = 2\cdot\sin(x)\cdot\cos(x)\) bzw.
\(\sin (x) = 2\cdot\sin(\frac{x}{2})\cdot\cos(\frac{x}{2})\)
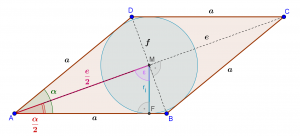
Wir wissen, dass sich bei der Raute die Diagonalen einander halbieren und auch die Diagonalen die Winkel halbieren (siehe Skizze).
Für den Inkreisradius ergibt sich aus dem rechtwinkeligen Dreieck \(\triangle AFM\) mit \(\frac{e}{2}\) als Hypothenuse und dem Inkreisradius als Gegenkathete des Winkels \(\frac{\alpha }{2}\)
\({{r}_{i}}=\frac{e}{2}\cdot \sin \left( {\frac{\alpha }{2}} \right)\)
Die Fläche des Inkreises beträgt demnach
\(\begin{array}{} A_{Inkreis}=r_{i}^{2}\cdot \pi \\ \quad\quad\quad =\left( \frac{e}{2}\cdot \sin \left( \frac{\alpha}{2} \right) \right)^{2}\cdot \pi \\ \quad\quad\quad =\frac{e^2}{4}\cdot \sin ^2\left( \frac{\alpha}{2} \right)\cdot \pi \end{array}\)
Aus dem Dreieck \(\triangle ABM\) ergibt sich ein Zusammenhang zwischen \(a\) und \(e\).
\(a\cdot \cos \left( {\frac{\alpha }{2}} \right)=\frac{e}{2}\quad \Rightarrow \quad e=2\cdot a\cdot \cos \left( {\frac{\alpha }{2}} \right)\)
Das kann man in die Flächenformel des Inkreises einsetzen und erhält
\(\begin{array}{l}{{A}_{{Inkreis}}}=\frac{{{{{\left( {2\cdot a\cdot \cos \left( {\frac{\alpha }{2}} \right)} \right)}}^{2}}}}{4}\cdot {{\sin }^{2}}\left( {\frac{\alpha }{2}} \right)\cdot \pi \\ \quad\quad\quad =\frac{{4\cdot {{a}^{2}}\cdot {{{\cos }}^{2}}\left( {\frac{\alpha }{2}} \right)}}{4}\cdot {{\sin }^{2}}\left( {\frac{\alpha }{2}} \right)\cdot \pi \\ \quad\quad\quad={{a}^{2}}\cdot {{\cos }^{2}}\left( {\frac{\alpha }{2}} \right)\cdot {{\sin }^{2}}\left( {\frac{\alpha }{2}} \right)\cdot \pi \end{array}\)
Dies sollte nun die halbe Fläche der Raute sein. Für die Fläche der Raute gilt
\(A_{Raute}=a\cdot h = a\cdot a\cdot \sin \alpha =a^2\cdot \sin \alpha \quad \Rightarrow \quad \frac{A_{Raute}}{2} = \frac{a^2\cdot \sin \alpha}{2}\)
Eingesetzt also
\({{a}^{2}}\cdot {{\cos }^{2}}\left( {\frac{\alpha }{2}} \right)\cdot {{\sin }^{2}}\left( {\frac{\alpha }{2}} \right)\cdot \pi =\frac{{{{a}^{2}}\cdot \sin \alpha }}{2}\quad \quad |:{{a}^{2}}\)
Das \(a^2\) kürzt sich weg und es bleibt als Bedingung
\({{\cos }^{2}}\left( {\frac{\alpha }{2}} \right)\cdot {{\sin }^{2}}\left( {\frac{\alpha }{2}} \right)\cdot \pi =\frac{{\sin \alpha }}{2}\)
Den \(\sin \alpha \) im Zähler der rechten Seite kann man schreiben als \(2\cdot \sin \left( {\frac{\alpha }{2}} \right)\cdot \cos \left( {\frac{\alpha }{2}} \right)\), daher folgt
\(\displaystyle \begin{array}{*{20}{l}} {{{{\cos }}^{2}}\left( {\frac{\alpha }{2}} \right)\cdot {{{\sin }}^{2}}\left( {\frac{\alpha }{2}} \right)\cdot \pi =\frac{{2\cdot \sin \left( {\frac{\alpha }{2}} \right)\cdot \cos \left( {\frac{\alpha }{2}} \right)}}{2}} \\ {{{{\cos }}^{2}}\left( {\frac{\alpha }{2}} \right)\cdot {{{\sin }}^{2}}\left( {\frac{\alpha }{2}} \right)\cdot \pi =\sin \left( {\frac{\alpha }{2}} \right)\cdot \cos \left( {\frac{\alpha }{2}} \right)\quad \quad |:\sin \left( {\frac{\alpha }{2}} \right)\quad :\cos \left( {\frac{\alpha }{2}} \right)} \\ {\cos \left( {\frac{\alpha }{2}} \right)\cdot \sin \left( {\frac{\alpha }{2}} \right)\cdot \pi =1} \end{array}\)
Auf der linken Seite mit 2 erweitert ergibt schließlich
\(\frac{{\overbrace{{2\cdot \cos \left( {\frac{\alpha }{2}} \right)\cdot \sin \left( {\frac{\alpha }{2}} \right)}}^{{=\,\,\sin \left( {2\cdot \frac{\alpha }{2}} \right)\,\,=\,\,\sin \alpha }}}}{2}\cdot \pi =1\quad \Rightarrow \quad \frac{{\sin \alpha }}{2}=\frac{1}{\pi }\quad \Rightarrow \quad \sin \alpha =\frac{2}{\pi }\)
\(\alpha = \sin^{-1}\left( \frac{2}{\pi } \right) \approx 39,54{}^\circ\)
Der Winkel \(\alpha\) der Raute muss \(\alpha \approx 39,54{}^\circ\) betragen, damit der Inkreis die halbe Fläche der Raute hat.
Es gibt einen alternativen Lösungsweg, der etwas kürzer und vielleicht eleganter ist.
Aus der Skizze sieht man folgende Zusammenhänge:
Die Fläche der Raute ist bekanntlich \(\displaystyle A_{Raute} = a\cdot h\)
Die Höhe der Raute ist aber der doppelte Inkreisdurchmesser (der Inkreis berührt ja unten und oben die jeweiligen Seiten \(\displaystyle a\)).
\(\displaystyle h = 2\cdot r_i \)
Daraus folgt die Fläche der Raute mit
\(\displaystyle A_{Raute} = 2\, a\, r_i\)
Die Fläche des Inkreises ist
\(\displaystyle A_{In} = r_i^2\, \pi\)
Die Fläche des Inkreises soll die halbe Fläche der Raute sein:
\(\displaystyle \begin{array}{l}r_{i}^{2}\pi =\frac{{2\,{{r}_{i}}\,a}}{2}\\{{r}_{i}}\,\pi =a\end{array}\)
Die Höhe der Raute ist im rechtwinkeligen Dreieck \(\displaystyle \triangle AED\) mit der Hypothenuse \(\displaystyle a\) aber die Gegenkathete zum Winkel \(\displaystyle \alpha\), also
\(\displaystyle h=a\sin \alpha \), also folgt
\(\displaystyle \begin{array}{l}a\sin \alpha =2\,{{r}_{i}}\\a=\frac{{2\,{{r}_{i}}}}{{\sin \alpha }}\end{array}\)
Das setzt man nun in \(\displaystyle {{r}_{i}}\,\pi =a\) ein und erhält
\(\displaystyle {{r}_{i}}\,\pi =\frac{{2\cdot {{r}_{i}}}}{{\sin \alpha }}\)
Das \(\displaystyle r_i\) kürzt sich, und die Umstellung nach \(\displaystyle \sin \alpha\) ergibt
\(\displaystyle \begin{array}{l}\pi =\frac{2}{{\sin \alpha }}\\\sin \alpha =\frac{2}{\pi }\end{array}\)
Daraus folgt schließlich
\(\displaystyle \alpha ={{\sin }^{{-1}}}\left( {\frac{2}{\pi }} \right)\approx 39,54{}^\circ \)