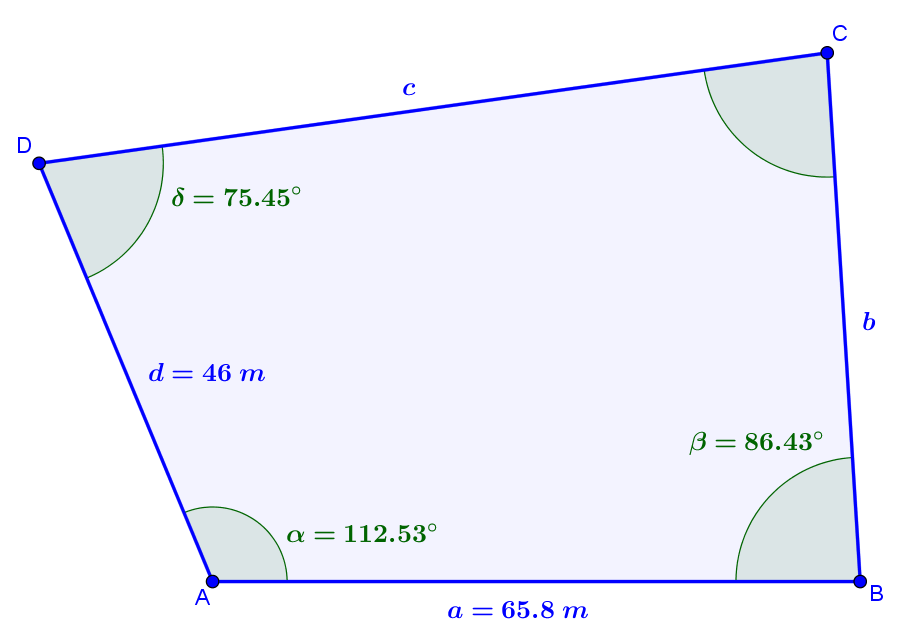
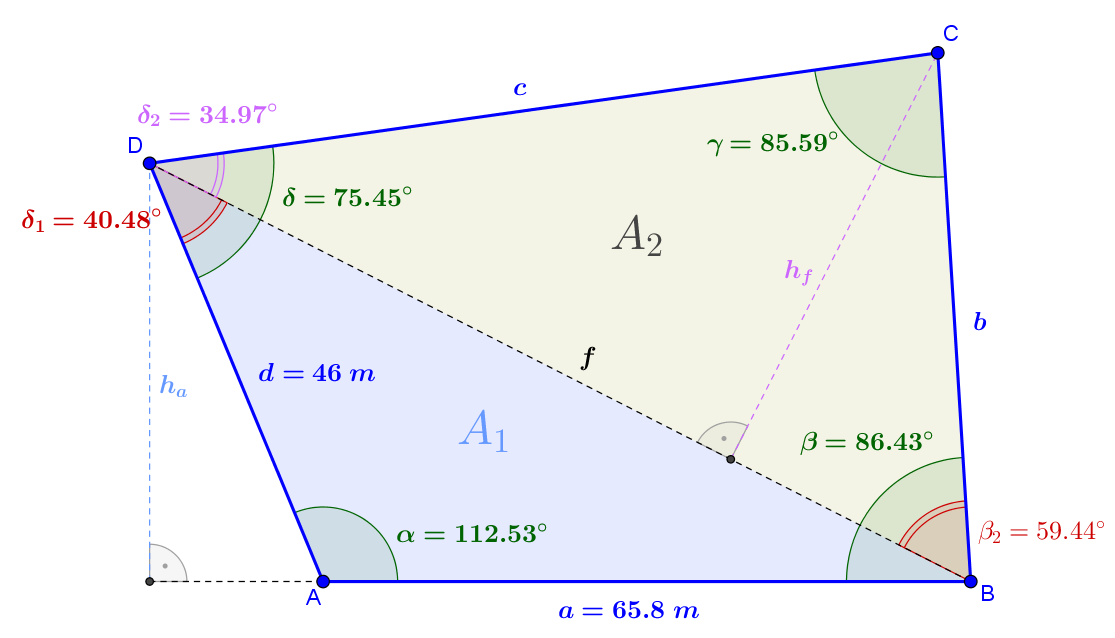
An einer Straßenkreuzung \(A\) liegt ein Grundstück \(ABCD\), dessen Straßenlängen \(a=\overline{{AB}}=65,8\,m\) und \(d=\overline{{AD}}=46\,m\) betragen. Die Grenzlinien an den Straßen schneiden sich unter einem Winkel von \(\alpha =112,53{}^\circ \). Man ermittelte von \(B\) und \(D\) aus die Winkel zum vierten Punkt \(C\) mit \(\beta =\angle CBA=86,43{}^\circ\) und \(\delta = \angle ADC =75,45{}^\circ\)
Gesucht: Welchen Flächeninhalt hat das Grundstück?
Benögtigte Kenntnisse:
- Gleichungen umformen
- Summensatz im Dreieck:
\(\alpha + \beta + \gamma = 180^{\circ}\) - Summensatz im Viereck:
\(\alpha + \beta + \gamma + \delta= 360^{\circ}\) - Sinus des Supplementärwinkels
- Trigonometrische Flächenformel im Dreieck
\(A=\frac{{c\cdot {{h}_{c}}}}{2}=\frac{{c\cdot b\cdot \sin \alpha }}{2}=\frac{{c\cdot a\cdot \sin \beta }}{2}\) - Sinussatz und Cosinussatz im allgemeinen Dreieck
Die Summe der Innenwinkel in einem Viereck ist immer 360°. Daher folgt für \(\gamma\)
\(\gamma =360{}^\circ -\alpha -\beta -\delta =360{}^\circ -112,53{}^\circ -86,43{}^\circ -75,45{}^\circ =85,59{}^\circ \)
Die Diagonale \(f\) teilt das Viereck in zwei Dreiecke. Mit den Seiten \(a\) und \(d\) sowie dem eingeschlossenen Winkel \(\alpha\) berechnet sich \(f\) mit dem Cosinussatz zu
\(\begin{array}{}f^{2}=a^{2}+d^{2}-2\cdot a\cdot d\cdot \cos (\alpha )={{65,8}^{2}}+{{46}^{2}}-2\cdot 65,8\cdot 46\cdot \cos (112,53)=8765,18\\f=\sqrt{{8765,18}}=93,62\,m\end{array}\)
Die Fläche \(A_1\) des unteren Dreiecks lässt sich mit der trigonometrischen Flächenformel sofort berechnen mit
\({{A}_{1}}=\frac{{a\cdot {{h}_{a}}}}{2}=\frac{{a\cdot d\cdot \sin \alpha }}{2}=\frac{{65,8\cdot 46\cdot \sin (112,53)}}{2}=1397,9\,{{m}^{2}}\)
Anmerkung: Hier wurde die Tatsache benutzt, dass der Sinus des Winkels \(\alpha\) gleich dem Sinus des Supplementärwinkel von \(\alpha\) ist: \(\sin \alpha = \sin (180^{\circ}-\alpha)\)
Alternativ kann auch die Flächenformel des Heron verwendet werden, da nun alle Seiten \(a,d,f\) bekannt sind. Der halbe Umfang lautet
\(\displaystyle {{s}_{1}}=\frac{{a+d+f}}{2}=\frac{{65,8+46+93,62}}{2}=102,71\,m\)
Damit ergibt sich
\(\displaystyle {{A}_{1}}=\sqrt{{{{s}_{1}}\cdot ({{s}_{1}}-a)\cdot ({{s}_{1}}-b)\cdot ({{s}_{1}}-f)}}=\)
\(\displaystyle =\sqrt{{102,71\cdot (102,71-65,8)\cdot (102,71-46)\cdot (102,71-93,62)}}=1397,9\,{{m}^{2}}\)
Die Fläche des oberen Dreiecks \(A_2\) ist komplizierter, wir benötigen noch eine Seite des oberen Dreiecks. Der Sinutzsatz liefert dort
\(\frac{c}{{\sin {{\beta }_{2}}}}=\frac{f}{{\sin \gamma }}\)
Aus dem unteren Dreieck \(A_1\) folgt mit dem Sinussatz
\(\frac{a}{{\sin {{\delta }_{1}}}}=\frac{f}{{\sin \alpha }}\quad \Rightarrow \quad \sin {{\delta }_{1}}=\frac{{a\cdot \sin \alpha }}{f}\quad \Rightarrow \quad {{\delta }_{1}}={{\sin }^{{-1}}}\left( {\frac{{65,8\cdot \sin (112,53)}}{{93,62}}} \right)=40,48{}^\circ \)
Daraus ergibt sich \({{\delta }_{2}}=\delta -{{\delta }_{1}}=75,45{}^\circ -40,48{}^\circ =34,97{}^\circ \)
und mit dem Summensatz im oberen Dreieck
\({{\beta }_{2}}=180{}^\circ -\gamma -{{\delta }_{2}}=180{}^\circ -85,59{}^\circ -34,97{}^\circ =59,44{}^\circ \) und damit
\(c=\frac{{f\cdot \sin {{\beta }_{2}}}}{{\sin \gamma }}=\frac{{93,62\cdot \sin (59,44)}}{{\sin (85,59)}}=80,86\,m\)
Nun kann man mit der Diagonale \(f\) und der Höhe \(h_f\) wieder die trigonometrische Flächenformel anwenden.
\({{h}_{f}}=c\cdot \sin {{\delta }_{2}}\)
\({{A}_{2}}=\frac{{f\cdot {{h}_{f}}}}{2}=\frac{{f\cdot c\cdot \sin {{\delta }_{2}}}}{2}=\frac{{93,62\cdot 80,86\cdot \sin (34,97)}}{2}=2169,4\,{{m}^{2}}\)
Die Fläche des gesamten Grundstücks beträgt damit
\({{A}_{{ges}}}={{A}_{1}}+{{A}_{2}}=1397,9\,{{m}^{2}}+2169,4\,{{m}^{2}}=3567,3\,{{m}^{2}}\)