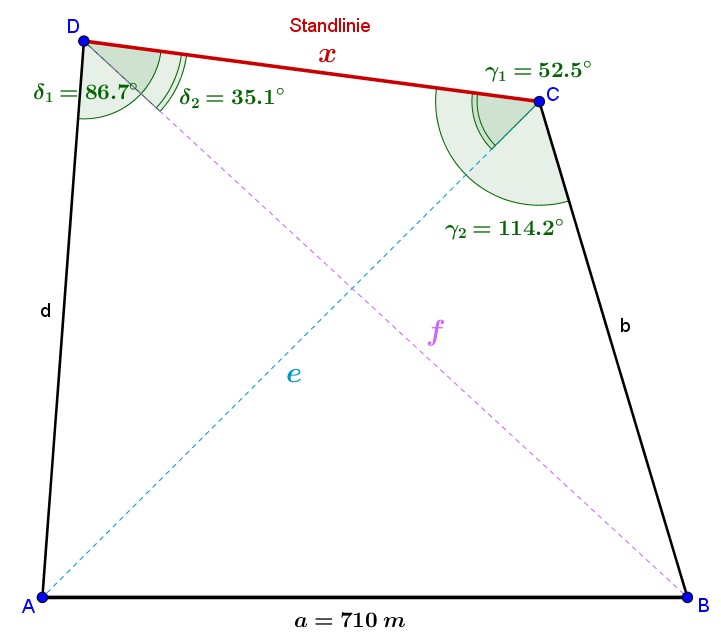
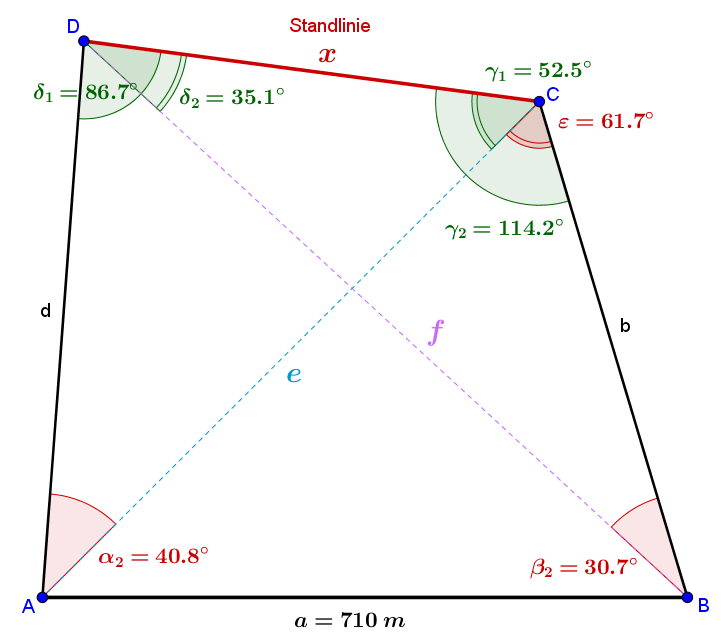
In Vermessungsaufgaben ist es oftmals notwendig eine unbekannte Strecke aus bekannten Strecken und Winkeln zu berechnen. Beim Verfahren “Rückwärts Einschneiden” möchte man die Länge einer Standlinie ermitteln, wenn diese aus irgendwelchen Gründen (keine Sicht) nicht direkt messbar ist. Man vermisst daher eine gegenüberliegende Strecke, und von der unbekannten Standlinie die Winkel zu den Endpunkten dieser gegenüberliegenden Strecke. Daraus kann die Länge der Standlinie berechnet werden.
Von den Endpunkten der nicht direkt messbaren Standlinie \(x\) werden zwei Punkte \(A,B\), deren Entfernung \(a=710\,m\) beträgt, anvisiert. Es werden dabei folgende Winkel gemessen:
\(\delta_1=86,7^{\circ}\), \(\delta_2=35,1^{\circ}\), \(\gamma_1=52,5^{\circ}\), \(\gamma_2=114,2^{\circ}\)
Gesucht: Berechne die Länge der unbekannten Standlinie \(x\).
Benögtigte Kenntnisse:
- Gleichungen umformen
- Summensatz im Dreieck:
\(\alpha + \beta + \gamma = 180^{\circ}\) - Sinussatz und Cosinussatz im allgemeinen Dreieck
Wir tun so, als wäre die Standlinie \(x\) bekannt und teilen die Figur in die beiden Dreiecke \(\triangle ACD\) und \(\triangle BCD\) auf.
Aus dem Summensatz ergeben sich zunächst die Winkel
\(\triangle ACD\): \({{\alpha }_{2}}=180{}^\circ -{{\delta }_{1}}-{{\gamma }_{1}}=180{}^\circ -86,7{}^\circ -52,5{}^\circ =40,8{}^\circ \)
\(\triangle BCD\): \({{\beta }_{2}}=180{}^\circ -{{\delta }_{2}}-{{\gamma }_{2}}=180{}^\circ -35,1{}^\circ -114,2{}^\circ =30,7{}^\circ \)
Außerdem ist \(\varepsilon\) gegeben durch
\(\varepsilon ={{\gamma }_{2}}-{{\gamma }_{1}}=114,2{}^\circ -52,5{}^\circ =61,7{}^\circ \)
Mit dem Sinussatz erhält man dann im \(\triangle BCD\)
\(\displaystyle \frac{b}{{\sin {{\delta }_{2}}}}=\frac{x}{{\sin {{\beta }_{2}}}}\quad \Rightarrow \quad b=\frac{{x\cdot \sin {{\delta }_{2}}}}{{\sin {{\beta }_{2}}}}\)
sowie im \(\triangle ACD\)
\(\displaystyle \frac{e}{{\sin {{\delta }_{1}}}}=\frac{x}{{\sin {{\alpha }_{2}}}}\quad \Rightarrow \quad e=\frac{{x\cdot \sin {{\delta }_{1}}}}{{\sin {{\alpha }_{2}}}}\)
Man beachte, dass die Seiten \(b,e\) unbekannt sind, da ja \(x\) unbekannt ist!
Mit diesen Seiten \(b,e\) und dem eingeschlossenen Winkel \(\varepsilon\) ergibt der Cosinussatz im \(\triangle ACB\)
\(\displaystyle {{a}^{2}}={{b}^{2}}+{{e}^{2}}-2\cdot b\cdot e\cdot \cos \varepsilon \)
Einsetzen der der Seiten \(b,e\) in den Cosinussatz ergibt
\(\displaystyle {{a}^{2}}={{\left( {\frac{{x\cdot \sin {{\delta }_{2}}}}{{\sin {{\beta }_{2}}}}} \right)}^{2}}+{{\left( {\frac{{x\cdot \sin {{\delta }_{1}}}}{{\sin {{\alpha }_{2}}}}} \right)}^{2}}-2\cdot \left( {\frac{{x\cdot \sin {{\delta }_{2}}}}{{\sin {{\beta }_{2}}}}\cdot \frac{{x\cdot \sin {{\delta }_{1}}}}{{\sin {{\alpha }_{2}}}}} \right)\cdot \cos \varepsilon \)
Die Quadrate ausgerechnet erhält man
\(\displaystyle {{a}^{2}}=\frac{{{{x}^{2}}\cdot {{{\sin }}^{2}}{{\delta }_{2}}}}{{{{{\sin }}^{2}}{{\beta }_{2}}}}+\frac{{{{x}^{2}}\cdot {{{\sin }}^{2}}{{\delta }_{1}}}}{{{{{\sin }}^{2}}{{\alpha }_{2}}}}-2\cdot {{x}^{2}}\cdot \frac{{\sin {{\delta }_{2}}\cdot \sin {{\delta }_{1}}}}{{\sin {{\beta }_{2}}\cdot \sin {{\alpha }_{2}}}}\cdot \cos \varepsilon \)
Nach dem Ausklammern von \(x^2\) ergibt sich
\(\displaystyle {{a}^{2}}={{x}^{2}}\cdot \left( {\frac{{{{{\sin }}^{2}}{{\delta }_{2}}}}{{{{{\sin }}^{2}}{{\beta }_{2}}}}+\frac{{{{{\sin }}^{2}}{{\delta }_{1}}}}{{{{{\sin }}^{2}}{{\alpha }_{2}}}}-2\cdot \frac{{\sin {{\delta }_{2}}\cdot \sin {{\delta }_{1}}}}{{\sin {{\beta }_{2}}\cdot \sin {{\alpha }_{2}}}}\cdot \cos \varepsilon } \right)\)
und damit
\(\displaystyle {{x}^{2}}=\frac{{{{a}^{2}}}}{{\left( {\frac{{{{{\sin }}^{2}}{{\delta }_{2}}}}{{{{{\sin }}^{2}}{{\beta }_{2}}}}+\frac{{{{{\sin }}^{2}}{{\delta }_{1}}}}{{{{{\sin }}^{2}}{{\alpha }_{2}}}}-2\cdot \frac{{\sin {{\delta }_{2}}\cdot \sin {{\delta }_{1}}}}{{\sin {{\beta }_{2}}\cdot \sin {{\alpha }_{2}}}}\cdot \cos \varepsilon } \right)}}\)
Sowohl \(a\) als auch alle Winkelwerte im Nenner sind bekannt. Zu beachten sind die Quadrate bei den Sinuswerten! Es ist fast unmöglich, diesen monströsen Ausdruck in einem Stück in den Taschenrechner einzugeben, ohne dabei einen Fehler zu machen…
Wir berechnen die Brüche im Nenner einzeln:
\(\displaystyle \frac{{{{{\sin }}^{2}}{{\delta }_{2}}}}{{{{{\sin }}^{2}}{{\beta }_{2}}}}=\frac{{{{{\sin }}^{2}}(35,1)}}{{{{{\sin }}^{2}}(30,7)}}\approx 1,2685\)
\(\displaystyle \frac{{{{{\sin }}^{2}}{{\delta }_{1}}}}{{{{{\sin }}^{2}}{{\alpha }_{2}}}}=\frac{{{{{\sin }}^{2}}(86,7)}}{{{{{\sin }}^{2}}(40,8)}}\approx 2,3344\)
\(\displaystyle \frac{{\sin {{\delta }_{2}}\cdot \sin {{\delta }_{1}}}}{{\sin {{\beta }_{2}}\cdot \sin {{\alpha }_{2}}}}=\frac{{\sin (35,1)\cdot \sin (86,7)}}{{\sin (30,7)\cdot \sin (40,8)}}\approx 1,7208\)
Damit ergibt sich
\(\displaystyle x^2=\frac{(710\,m)^2}{\left( {1,2685+2,3344-2\cdot 1,7208\cdot \cos (61,7)} \right)}=255722,4\,m^2\)
\(\displaystyle x=\sqrt{255722,4\,m^2}=505,7\,m\)
Die Länge der Standlinie beträgt \(x=505,7\,m\)