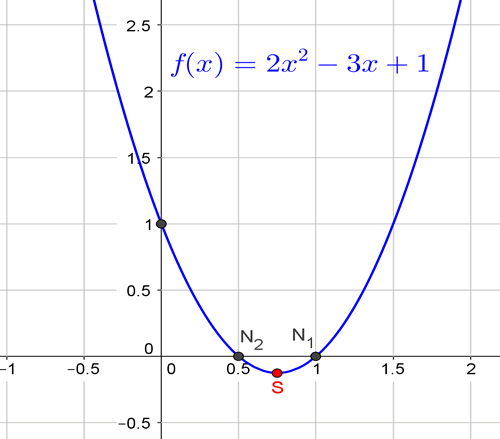
Gegeben sei die quadratische Funktion \(f(x)=2x^2-3x+1\)
- Berechne die Nullstellen dieser Funktion.
- Gibt die Koordinaten des Scheitelpunktes \(S\) an.
- Zeichne den Graphen der Funktion und beschrifte die Nullstellen und den Scheitelpunkt.
1.) Nullstellen
Die Nullstellen einer Funktion erhält man, indem man \(f(x)= 0\) setzt und jene Werte für \(x\) berechnet, bei denen das zutrifft. Mit anderen Worten, man muss die quadratische Gleichung \(f(x)=2x^2-3x+1 = 0\) lösen.
Die allgemeine Form der quadratischen Funktion lautet: \(f(x)=ax^2+bx+c\).
Allgemein: \(f(x)=ax^2+bx+c\)
Unsere Gleichung: \(f(x)=2x^2-3x+1\)
Wir vergleichen die Zahlen und schreiben in unserem Fall:
\(a = 2, b = -3, c = 1\)
Nun setzen wir diese Werte in die bekannte “Mitternachtsformel” ein: \(x_{1,2} = \frac{-b \pm \sqrt{b^2-4 a c} }{2a}\)
\(x_{1,2} = \frac{-(-3) \pm \sqrt{(-3)^2 – 4(2\cdot 1)} }{2\cdot2} = \frac{3 \pm \sqrt{9 – 8} }{4} = \frac{3 \pm \sqrt{1} }{4} = \frac{3 \pm 1 }{4}\)
\(x_1 = \frac{3+1}{4} = \frac{4}{4} = 1\)
\(x_2 = \frac{3-1}{4} = \frac{2}{4} = \frac{1}{2}\)
Nullstellen sind also \(N_1 = (1|0)\) und \(N_2 = (\frac{1}{2}|0)\)
2.) Scheitelpunkt
Der Scheitelpunkt hat die Koordinaten \(S = \left( \frac{-b}{2a} | c – \frac{b^2}{4a} \right)\)
Wir setzen für a, b, c unsere Werte ein und erhalten
\(S = \left( \frac{-(-3)}{2\cdot2} | 1 – \frac{(-3)^2}{4\cdot2} \right) = \left( \frac{3}{4} | 1 – \frac{9}{8} \right) = \left( \frac{3}{4} | -\frac{1}{8} \right)\)
Der Scheitelpunkt der Parabel liegt bei \(S = \left( \frac{3}{4} | -\frac{1}{8} \right)\)
3.) Graph der Funktion