Nachstehend findet man einige Rätsel, die zur Schärfung der mathematischen Fähigkeiten dienen sollen. Man sollte versuchen, die Aufgaben selbstständig zu lösen, manchmal bekommt man auch Tipps oder eine kleine Hilfestellung. Die Beispiele beschäftigen sich vor allem mit Geometrie.
Es geht um das visuelle Erkennen der gestellten Aufgabe und der daraus resultierenden mathematischen Formulierung. Hat man die mathematischen Zusammenhänge gefunden, ist noch das konkrete Ausrechnen notwendig.
Diese „Fingerübungen“ können das praktische Rechnen erheblich verbessern! Man sollte wirklich versuchen, die Beispiele zuerst selbstständig zu lösen. Bei jedem Beispiel ist eine Musterlösung enthalten. Es kann aber durchaus sein, dass es eine alternative Lösungsmöglichkeit gibt, welche zum selben Ergebnis führt.
Mathematische Rätselaufgaben
Gegeben: In einem Kreis mit dem Radius \(R=8\) befindet sich ein kleinerer Kreis, der den größeren im Punkt \(P\) berührt. Ein weiterer Berührpunkt \(S\) liegt auf der waagrechten Strecke \(\overline{MQ}\) und teilt diese in der Hälfte.
Gesucht: Radius \(r\) des kleineren Kreises (rot).
Gegeben: Von einer Raute \(ABCD\) mit der Seitenlänge \(a\) ist bekannt, dass ihr Inkreis die halbe Fläche der Raute hat.
Gesucht: Berechne den Winkel \(\alpha\) beim Punkt \(A\) der Raute, damit diese Bedingung erfüllt ist!
Gegeben: Ein gleichseitiges Dreieck \(\triangle ABC\) mit der Seitenlänge \(s=2\), mit einem Quadrat bei Punkt \(B\) mit der Seitenlänge \(1\). Die obere Seite des Quadrats schneidet die Seite \(BC\) im Punkt \(E\), die Verbindung \(AE\) schneidet die Höhe \(h\) des Dreiecks im Punkt \(F\).
Gesucht: Der Inkreisradius \(r_i\) des Dreiecks \(\triangle ABF\) (in der Skizze rot).
Gegeben: Einem rechtwinkeligen Dreieck mit den Katheten \(3,4\) und der Hypothenuse \(5\) sind zwei Kreise eingeschrieben, die einander berühren. Die Kreise sind kongruent (flächengleich) und berühren beide die Hypothenuse. Der obere Kreis berührt die kurze Kathete \(3\), der untere die lange Kathete \(4\).
Gesucht: Der Radius \(r\) der Kreise
Lösungsdatei in Bearbeitung....
Gegeben: In eine Parabel mit der Gleichung \(f(x)=\frac{1}{8}x^2\) "fällt" von oben ein Kreis mit dem Radius \(r=8\), bis er die Parabel an den Punkten \(P,P^{\prime}\) berührt.
Gesucht: Die Koordinaten des Kreismittelpunkts \(M\).
Lösungsdatei in Bearbeitung....
Angewandte Mathematik
Dies ist ein Beispiel aus der Zentralmatura 2016
Ein Unternehmen, das Skate-Parks errichtet, plant eine neue Minirampe.
Das seitliche Profil der Rampe kann durch eine Parabel 2. Ordnung modelliert werden:
\(f(x)=0,2\cdot {{x}^{2}}-2\cdot x+4,95\quad \quad mit\quad 1,5<x<4,5\)
\(x...\) waagrechte Entfernung von der Rückwand in Metern (m)
\(f(x)...\) Höhe der Rampe in Metern (m) an der Stelle \(x\)
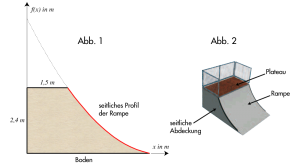
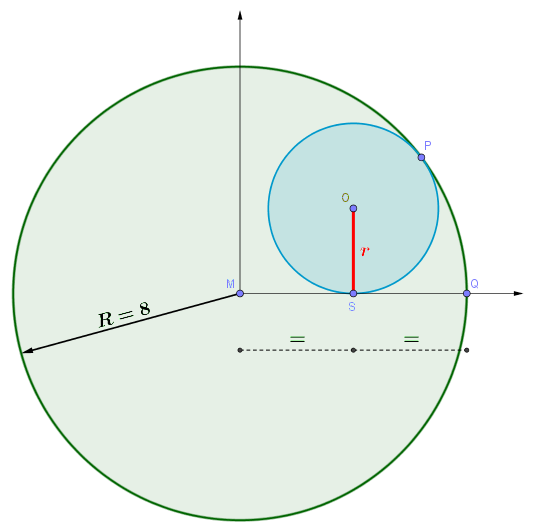
- Berechnen Sie den Inhalt der Querschnittsfläche einer seitlichen Abdeckung.
Entnehmen Sie die dazu notwendigen Werte der Abbildung 1. - Zeigen Sie, dass die gegebene Parabel 2. Ordnung beim Übergang zum Boden keine waagrechte Tangente aufweist.
- Dokumentieren Sie die Berechnung des Winkels zwischen Plateau und Rampe.
- Auf Kundenwunsch wird eine höhere Rampe errichtet, deren seitliches Profil wieder durch eine quadratische Funktion \(f\) mit \(f(x)=a\cdot {{x}^{2}}+b\cdot x+c\) beschrieben werden kann.
Höhe der Rampe: 3 m
Tiefe des Plateaus: 1,5 m
maximales Gefälle: 100 %
Bodenlänge der Rampe: 6,5 m
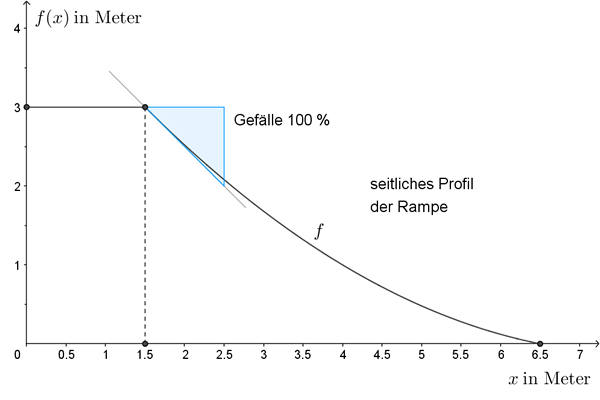
– Stellen Sie mit den gegebenen Angaben ein Gleichungssystem zur Berechnung der
Koeffizienten dieser quadratischen Funktion auf.
Hinweis zur Aufgabe:
Lösungen müssen der Problemstellung entsprechen und klar erkennbar sein. Ergebnisse sind
mit passenden Maßeinheiten anzugeben.